Question

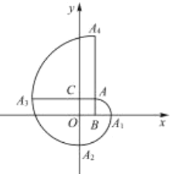
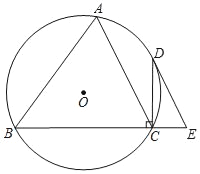
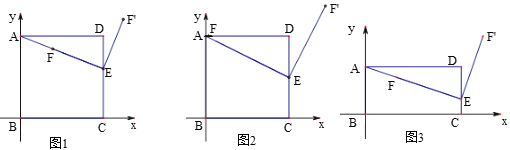
【题目】正方形ABCD的边长为4，以B为原点建立如图1平面直角坐标系中，E是边CD上的一个动点，F是线段AE上一点，将线段EF绕点E顺时针旋转90°得到EF'.

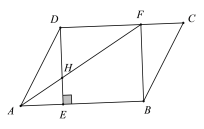
(1)如图2，当E是CD中点，时，求点F'的坐标.

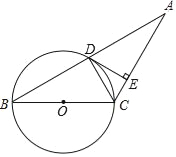
(2)如图1，若，且F'，D，B在同一直线上时，求DE的长.

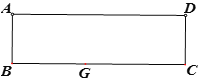
(3)如图3，将正边形ABCD改为矩形，AD=4，AB=2，其他条件不变，若，且F'，D，B在同一直线上时，则DE的长是_______.(请用含n的代数式表示)

Answer 1

【答案】(1)点F'的坐标是(6，6)；(2)；(3)

【解析】

（1）如图2，作EM⊥AB于M，交CD延长线于H，证明△AME≌△F'HE，求出AM=F'H=2，EM=EH=4，即可解决问题；

（2）如图1，作FM⊥CD于M，F'H⊥CD交CD延长线于H，连接BF'，设DE=x，首先证明FM是三角形的中位线，再利用全等三角形的性质构建方程即可解决问题；

（3）如图3，作FM⊥CD于M，F'H⊥CD交CD延长线于H，连接BF'，设DE=x，AE=1，AF=n，利用平行线分线段成比例求出FM，EM，再利用全等三角形的性质求出EH，H F'，再根据三角函数求出DH，构建方程即可解决问题.

解：（1）如图2，作EM⊥AB于M，交CD延长线于H，

∵E是CD中点，

∴四边形AMED是矩形，

∵∠AME=∠AEF'=∠MEH=∠H=90°，

∴∠AEM+∠AEH=90°，∠AEH+∠HEF'=90°，

∴∠AEM=∠HEF'，EA= EF'，

∴△AME≌△F'HE，

∴AM=F'H=2，EM=EH=4，

∴F'(6，6)；

（2）如图1，作FM⊥CD于M，F'H⊥CD交CD延长线于H，连接BF'，设DE=x，

∵，

∴AF=EF，

∵FM∥AD，∴DM=ME=，FM =，

∠AEM+∠HEF'=90°，∠AEM+∠MFE=90°，

∴∠HEF'=∠MFE，

因为∠FME=∠HF'E=90°，EF= EF'，

∴△FME≌△EHF'，

∴HF'=ME=，EH=FM=2，

∵四边形ABCD是正方形，

∴∠HDF'=∠BDC=45°，

∴DH= HF'=，

∴，

解得，

∴DE=.

（3）如图3，作FM⊥CD于M，F'H⊥CD交CD延长线于H，连接BF'，设DE=x，AE=1，AF=n，

∵FM∥AD，∴，

∴FM=4-4n，EM=x-xn，

由（2）可知△FME≌△EHF'，

∴HF'=EM=x-xn，EH=FM=4-4n，

∵，

∴DH=，

∴，

∴，

即.