Question

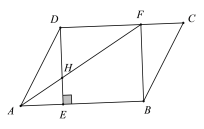
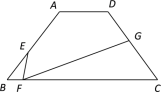
【题目】如图，在梯形ABCD中，，，，，点E为AB边上一点，且．点F是BC边上的一个动点（与点B、点C不重合），点G在射线CD上，且．设BF的长为x，CG的长为y．

（1）当点G在线段DC上时，求y与x之间的函数关系式，并写出自变量x的取值范围；

（2）当以点B为圆心，BF长为半径的⊙B与以点C为圆心，CG长为半径的⊙C相切时，求线段BF的长；

（3）当为等腰三角形时，直接写出线段BF的长．

Answer 1

【答案】（1），；（2）当⊙B与⊙C相切时，线段BF的长为：2或4或6；（3）当△FCG为等腰三角形时，线段BF的长为 或2或.

【解析】

（1）根据梯形的性质得到∠B＝∠C，进行证明∠GFC＝∠FEB，得到△EBF∽△FCG，根据相似三角形的性质得到，即可求出y与x之间的函数关系式.

（2）分两种情况:①当⊙B与⊙C外切时， BF＋CG＝BC；②当⊙B与⊙C内切时， CG－BF＝BC进行讨论即可.

（3）分三种情况进行讨论即可.

（1）∵梯形ABCD中，AD∥BC，AB＝DC

∴∠B＝∠C

∵∠EFC=∠B＋∠BEF＝=∠EFG＋∠GFC，∠EFG＝∠B

∴∠GFC＝∠FEB

∴△EBF∽△FCG

∴，∴

∴

自变量x的取值范围为：

（2）当，都有

，

①当⊙B与⊙C外切时， BF＋CG＝BC

∴，解得x＝2或x＝12（舍去）

②当⊙B与⊙C内切时， CG－BF＝BC

∴，解得x＝4或x＝6

综上所述，当⊙B与⊙C相切时，线段BF的长为：2或4或6

（3）当△FCG为等腰三角形时，线段BF的长为： 或2或