Question

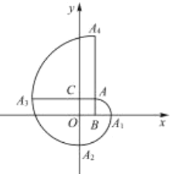
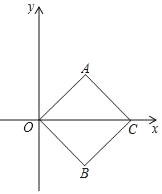
【题目】如图，四边形AOBC是正方形，点C的坐标是（4，0）．

（Ⅰ）正方形AOBC的边长为　 　，点A的坐标是　 　．

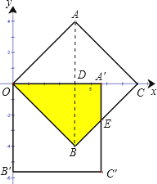
（Ⅱ）将正方形AOBC绕点O顺时针旋转45°，点A，B，C旋转后的对应点为A′，B′，C′，求点A′的坐标及旋转后的正方形与原正方形的重叠部分的面积；

（Ⅲ）动点P从点O出发，沿折线OACB方向以1个单位/秒的速度匀速运动，同时，另一动点Q从点O出发，沿折线OBCA方向以2个单位/秒的速度匀速运动，运动时间为t秒，当它们相遇时同时停止运动，当△OPQ为等腰三角形时，求出t的值（直接写出结果即可）．

Answer 1

【答案】（1）4，；（2）旋转后的正方形与原正方形的重叠部分的面积为；（3）.

【解析】

（1）连接AB，根据△OCA为等腰三角形可得AD=OD的长，从而得出点A的坐标，则得出正方形AOBC的面积；
（2）根据旋转的性质可得OA′的长，从而得出A′C，A′E，再求出面积即可；
（3）根据P、Q点在不同的线段上运动情况，可分为三种列式①当点P、Q分别在OA、OB时，②当点P在OA上，点Q在BC上时，③当点P、Q在AC上时，可方程得出t．

解：（1）连接AB，与OC交于点D，

四边形是正方形，
∴△OCA为等腰Rt△，

∴AD=OD=OC=2，
∴点A的坐标为.

4，.

（2）如图

∵ 四边形是正方形，

∴，.

∵ 将正方形绕点顺时针旋转，

∴ 点落在轴上.

∴.

∴ 点的坐标为.

∵，

∴.

∵ 四边形，是正方形，

∴，.

∴，.

∴.

∴.

∵，

，

∴ .

∴旋转后的正方形与原正方形的重叠部分的面积为.

（3）设t秒后两点相遇，3t=16，∴t=

①当点P、Q分别在OA、OB时，

∵,OP=t，OQ=2t

∴不能为等腰三角形

②当点P在OA上，点Q在BC上时如图2，

当OQ=QP，QM为OP的垂直平分线，
OP=2OM=2BQ，OP=t，BQ=2t-4，
t=2（2t-4），
解得：t=．

③当点P、Q在AC上时，

不能为等腰三角形

综上所述，当时是等腰三角形