��Ŀ����
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���֪������y=ax2+bx��5��x�ύ��A����1��0����B��5��0�����㣬��y�ύ�ڵ�C��
��1���������ߵĺ�������ʽ��
��2������D��y���ϵ�һ�㣬����B��C��DΪ��������������ABC���ƣ����D�����ꣻ
��3����ͼ2��CE��x�����������ཻ�ڵ�E����H��ֱ��CE�·��������ϵĶ��㣬����H����y��ƽ�е�ֱ����BC��CE�ֱ��ڵ�F��G����̽������H�˶����δ�ʱ���ı���CHEF�����������H�����꼰��������
��4������KΪ�����ߵĶ��㣬��M��4��m���Ǹ��������ϵ�һ�㣬��x�ᣬy���Ϸֱ��ҵ�P��Q��ʹ�ı���PQKM���ܳ���С�������P��Q�����꣮
���𰸡�
��1��
�⣺�ߵ�A����1��0����B��5��0����������y=ax2+bx��5�ϣ�
�� ![]() ��
��
�� ![]() ��
��
�������ߵı���ʽΪy=x2��4x��5
��2��
�⣺��ͼ1����x=0����y=��5��
��C��0����5����
��OC=OB��
���OBC=��OCB=45�㣬
��AB=6��BC=5 ![]() ��
��
Ҫʹ��B��C��DΪ��������������ABC���ƣ����� ![]() ��
�� ![]() ��
��
�ٵ� ![]() ʱ��
ʱ��
CD=AB=6��
��D��0��1����
�ڵ� ![]() ʱ��
ʱ��
�� ![]() ��
��
��CD= ![]() ��
��
��D��0�� ![]() ����
����
����D��������0��1����0�� ![]() ��
��

��3��
�⣺��H��t��t2��4t��5����
��CE��x�ᣬ
���E����������5��
��E���������ϣ�
��x2��4x��5=��5����x=0���ᣩ��x=4��
��E��4����5����
��CE=4��
��B��5��0����C��0����5����
��ֱ��BC�Ľ���ʽΪy=x��5��
��F��t��t��5����
��HF=t��5����t2��4t��5��=����t�� ![]() ��2+
��2+ ![]() ��
��
��CE��x�ᣬHF��y�ᣬ
��CE��HF��
��S�ı���CHEF= ![]() CEHF=��2��t��
CEHF=��2��t�� ![]() ��2+
��2+ ![]() ��
��
��t= ![]() ʱ���ı���CHEF��������Ϊ
ʱ���ı���CHEF��������Ϊ ![]()
��4��
�⣺��ͼ2����KΪ�����ߵĶ��㣬
��K��2����9����
��K����y��ĶԳƵ�K'����2����9����
��M��4��m�����������ϣ�
��M��4����5����
���M����x��ĶԳƵ�M'��4��5����
��ֱ��K'M'�Ľ���ʽΪy= ![]() x��
x�� ![]() ��
��
��P�� ![]() ��0����Q��0����
��0����Q��0���� ![]() ����
����
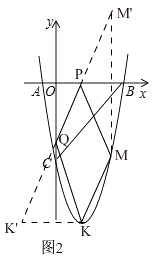
����������1�����ݴ���ϵ����ֱ�������߽���ʽ����2��������������������������εı���ʽ���������D�����ꣻ��3�������ֱ��BC�Ľ���ʽ����������ı���CHEF������ĺ�����ϵʽ������������ֵ����4�����öԳ����ҳ���P��Q��λ�ã��������P��Q�����꣮
�����㾫����������Ҫ�����˶��κ��������ʺ����������ε����ʵ����֪ʶ�㣬��Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С����Ӧ����ȣ���Ӧ�߳ɱ��������������ν������������β�����ȷ�����⣮