Question

【题目】如图1，一张矩形纸片ABCD，其中AD=8cm，AB=6cm，先沿对角线BD对折，点C落在点C′的位置，BC′交AD于点G．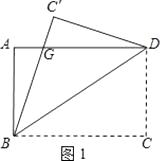
（1）求证：AG=C′G；
（2）如图2，再折叠一次，使点D与点A重合，得折痕EN，EN交AD于点M，求EM的长．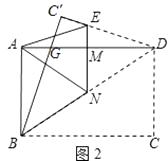

Answer 1

【答案】
（1）证明：∵沿对角线BD对折，点C落在点C′的位置，

∴∠A=∠C′，AB=C′D

∴在△GAB与△GC′D中，

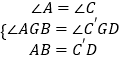
∴△GAB≌△GC′D

∴AG=C′G

（2）解：∵点D与点A重合，得折痕EN，

∴DM=4cm，

∵AD=8cm，AB=6cm，

在Rt△ABD中，BD= =10cm，

∵EN⊥AD，AB⊥AD，

∴EN∥AB，

∴MN是△ABD的中位线，

∴DN= BD=5cm，

在Rt△MND中，

∴MN= =3（cm），

由折叠的性质可知∠NDE=∠NDC，

∵EN∥CD，

∴∠END=∠NDC，

∴∠END=∠NDE，

∴EN=ED，设EM=x，则ED=EN=x+3，

由勾股定理得ED2=EM2+DM2，即（x+3）2=x2+42，

解得x= ，即EM= cm．

【解析】（1）通过证明△GAB≌△GC′D即可证得线段AG、C′G相等；（2）在直角三角形DMN中，利用勾股定理求得MN的长，则EN﹣MN=EM的长．
【考点精析】关于本题考查的矩形的性质和翻折变换（折叠问题），需要了解矩形的四个角都是直角，矩形的对角线相等；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能得出正确答案．