题目内容
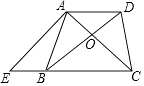
【题目】图1、图2为同一长方体房间的示意图，图3为该长方体的表面展开图． 
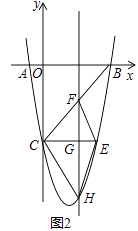
（1）蜘蛛在顶点A′处． ①苍蝇在顶点B处时，试在图1中画出蜘蛛为捉住苍蝇，沿墙面爬行的最近路线．
②苍蝇在顶点C处时，图2中画出了蜘蛛捉住苍蝇的两条路线，往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC，试通过计算判断哪条路线更近．
（2）在图3中，半径为10dm的⊙M与D′C′相切，圆心M到边CC′的距离为15dm，蜘蛛P在线段AB上，苍蝇Q在⊙M的圆周上，线段PQ为蜘蛛爬行路线，若PQ与⊙M相切，试求PQ长度的范围．
【答案】
（1）解：①根据“两点之间，线段最短”可知：
线段A′B为最近路线，如图1所示．
②（i）．将长方体展开，使得长方形ABB′A′和长方形ABCD在同一平面内，如图2①．
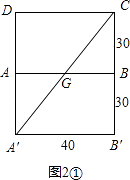
在Rt△A′B′C中，
∠B′=90°，A′B′=40，B′C=60，
∴AC= 
= 
=20 
．
(ii)．将长方体展开，使得长方形ABB′A′和长方形BCC′B′在同一平面内，如图2②．
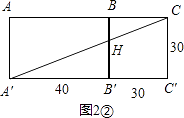
在Rt△A′C′C中，
∠C′=90°，A′C′=70，C′C=30，
∴A′C= 
= 
=10 
．
∵ ＜ ，
∴往天花板ABCD爬行的最近路线A′GC更近
（2）解：过点M作MH⊥AB于H，连接MQ、MP、MA、MB，如图3．
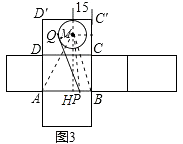
∵半径为10dm的⊙M与D′C′相切，圆心M到边CC′的距离为15dm，BC′=60dm，
∴MH=60﹣10=50，HB=15，AH=40﹣15=25，
根据勾股定理可得AM= 
= 
= 
，
MB= 
= 
= 
，
∴50≤MP≤ ．
∵⊙M与PQ相切于点Q，
∴MQ⊥PQ，∠MQP=90°，
∴PQ= 
= 
．
当MP=50时，PQ= 
=20 
；
当MP= 时，PQ= 
=55．
∴PQ长度的范围是20 dm≤PQ≤55dm
【解析】（1）①根据“两点之间，线段最短”可知：线段A′B为最近路线； ②(i)．将长方体展开，使得长方形ABB′A′和长方形ABCD在同一平面内，如图2①，运用勾股定理求出AC长；(ii)．将长方体展开，使得长方形ABB′A′和长方形BCC′B′在同一平面内，如图2②，运用勾股定理求出A′C长，然后将两个长度进行比较，就可解决问题；（2）过点M作MH⊥AB于H，连接MQ、MP、MA、MB，如图3．由⊙M与PQ相切于点Q可得MQ⊥PQ，即∠MQP=90°，根据勾股定理可得PQ= = ．要求PQ的取值范围，只需先求出MP的取值范围，就可解决问题．
【考点精析】关于本题考查的几何体的展开图和线段的基本性质，需要了解沿多面体的棱将多面体剪开成平面图形，若干个平面图形也可以围成一个多面体；同一个多面体沿不同的棱剪开，得到的平面展开图是不一样的，就是说：同一个立体图形可以有多种不同的展开图；线段公理：所有连接两点的线中，线段最短．也可简单说成：两点之间线段最短；连接两点的线段的长度，叫做这两点的距离；线段的大小关系和它们的长度的大小关系是一致的才能得出正确答案．
