题目内容
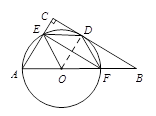
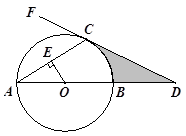
如图,在Rt△ABC中,∠C为直角,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
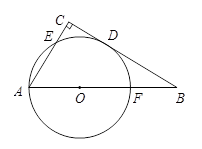
小题1:若AC=8,AB=12,求⊙O的半径;
小题2:连接OE、ED、DF、EF.若四边形BDEF是平行四边形,试判断四边形OFDE的形状,并说明理由

小题1:若AC=8,AB=12,求⊙O的半径;
小题2:连接OE、ED、DF、EF.若四边形BDEF是平行四边形,试判断四边形OFDE的形状,并说明理由
小题1:设⊙O的半径为r.
∵BC切⊙O于点D ∴OD⊥BC
∵∠C=90° ∴OD∥AC ∴△OBD∽△ABC. …………………………2分
∴
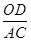 =
= 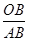 ,即
,即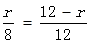 解得:
解得: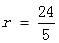
∴⊙O的半径为
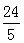 ………………………4分
………………………4分小题2:四边形OFDE是菱形 ………………5分
∵四边形BDEF是平行四边形 ∴∠DEF=∠B.
∵∠DEF=
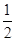 ∠DOB∴∠B=
∠DOB∴∠B=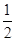 ∠DOB.
∠DOB.∵∠ODB=90° ∴∠DOB+∠B=90° ∴∠DOB=60°
∵DE∥AB,∴∠ODE=60°.∵OD=OE,∴△ODE是等边三角形
∴OD=DE∵OD=OF∴DE=OF∴四边形OFDE是平行四边形 ………7分
∵OE=OF∴平行四边形OFDE是菱形. …………………………………8分
(1)连接OD,设⊙O的半径为r,可证出△BOD∽△BAC,则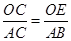 ,从而求得r;(2)由四边形BDEF是平行四边形,得∠DEF=∠B,再由圆周角定理可得,∠B=
,从而求得r;(2)由四边形BDEF是平行四边形,得∠DEF=∠B,再由圆周角定理可得,∠B= 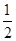 ∠DOB,则△ODE是等边三角形,先得出四边形OFDE是平行四边形.再根据OE=OF,则平行四边形OFDE是菱形.
∠DOB,则△ODE是等边三角形,先得出四边形OFDE是平行四边形.再根据OE=OF,则平行四边形OFDE是菱形.
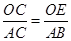 ,从而求得r;(2)由四边形BDEF是平行四边形,得∠DEF=∠B,再由圆周角定理可得,∠B=
,从而求得r;(2)由四边形BDEF是平行四边形,得∠DEF=∠B,再由圆周角定理可得,∠B= 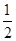 ∠DOB,则△ODE是等边三角形,先得出四边形OFDE是平行四边形.再根据OE=OF,则平行四边形OFDE是菱形.
∠DOB,则△ODE是等边三角形,先得出四边形OFDE是平行四边形.再根据OE=OF,则平行四边形OFDE是菱形.
练习册系列答案
相关题目
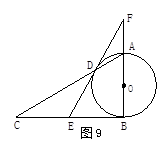
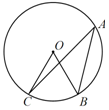
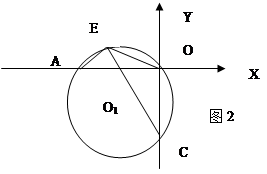
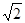 -1,直线l y=-X-
-1,直线l y=-X-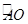 上一点,连接EC,EA.EO,当点E在劣弧
上一点,连接EC,EA.EO,当点E在劣弧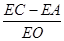 的值是否发生变化?如果不变,求其值,如果变化,说明理由.
的值是否发生变化?如果不变,求其值,如果变化,说明理由. 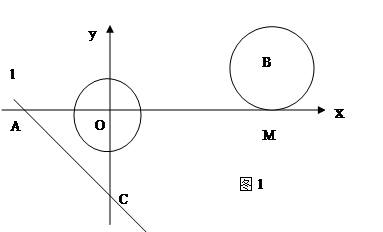 .
. 

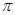 cm,则此扇形的面积为___________.
cm,则此扇形的面积为___________.