题目内容
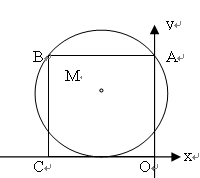
如图（2），在直角坐标系中，四边形OABC为正方形，顶点A、C在坐标轴上，以边AB为弦的⊙M与x轴相切，若点A的坐标为（0，8），则圆心M的坐标为( )
A、（4，5） B、（－5，4） C、（－4，6） D、（－4，5）
A、（4，5） B、（－5，4） C、（－4，6） D、（－4，5）
D
过点M作MD⊥AB于D，连接AM，设⊙M的半径为R，
∵四边形OABC为正方形，顶点A，C在坐标轴上，以边AB为弦的⊙M与x轴相切，点A的坐标为（0，8），
∴DA=4，AB=8，DM=8-R，AM=R，
又∵△ADM是直角三角形，根据勾股定理可得AM2=DM2+AD2，∴R2=（8-R）2+42，
解得R=5，∴M（-4，5）．故选D
∵四边形OABC为正方形，顶点A，C在坐标轴上，以边AB为弦的⊙M与x轴相切，点A的坐标为（0，8），
∴DA=4，AB=8，DM=8-R，AM=R，
又∵△ADM是直角三角形，根据勾股定理可得AM2=DM2+AD2，∴R2=（8-R）2+42，
解得R=5，∴M（-4，5）．故选D
练习册系列答案
高中必刷题系列答案
相关题目
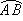的中点，判断四边形OACB的形状并证明你的结论.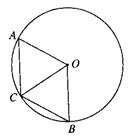
）.
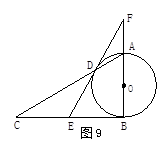