题目内容
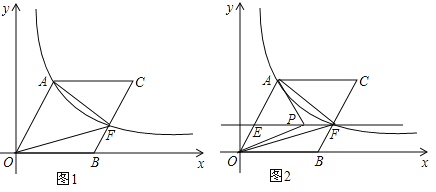
【题目】在平面直角坐标系中,O为坐标原点,B在x轴上,四边形OACB为平行四边形,且∠AOB=60°,反比例函数![]() (k>0)在第一象限内过点A,且与BC交于点F.(1)若OA=10,求反比例函数的解析式;
(k>0)在第一象限内过点A,且与BC交于点F.(1)若OA=10,求反比例函数的解析式;
(2)若F为BC的中点,且S△AOF=24![]() ,求OA长及点C坐标;
,求OA长及点C坐标;
(3)在(2)的条件下,过点F作EF∥OB交OA于点E(如图2),若点P是直线EF上一个动点,连结,PA,PO,问是否存在点P,使得以P,A,O三点构成的三角形是直角三角形?若存在,请指出这样的P点有几个,并直接写出其中二个P点坐标;若不存在,请说明了理由.
【答案】(1)反比例函数解析式:y=![]() (x>0);(2)C(
(x>0);(2)C(![]() );(3)P1(
);(3)P1(![]() ),P2(
),P2(![]() ),P3(
),P3(![]() ),P4(
),P4(![]() )
)
【解析】分析:(1)先过点A作AH⊥OB,根据∠AOB=60°,OA=10,求出AH和OH的值,从而得出A点坐标,再把它代入反比例函数中,求出k的值,即可求出反比例函数的解析式;
(2)先设OA=a(a>0),过点F作FM⊥x轴于M,根据∠AOB=60°,得出AHAH=![]() a,OH=
a,OH=![]() a,求出S△AOH的值,根据S△AOF=24
a,求出S△AOH的值,根据S△AOF=24![]() ,求出平行四边形AOBC的面积,根据F为BC的中点,求出S△OBF=12
,求出平行四边形AOBC的面积,根据F为BC的中点,求出S△OBF=12![]() ,最后根据S平行四边形AOBC=OBAH,得出OB=AC=12,即可求出点C的坐标;
,最后根据S平行四边形AOBC=OBAH,得出OB=AC=12,即可求出点C的坐标;
(3)分别根据当∠APO=90°时,在OA的两侧各有一点P,得出P1,P2;当∠PAO=90°时,求出P3;当∠POA=90°时,求出P4即可.
详解:
(1)过点A作AH⊥OB于H,
∵∠AOB=60°,OA=10,
∴AH=![]() ,OH=5,∴A点坐标为(5,
,OH=5,∴A点坐标为(5,![]() ),根据题意得:
),根据题意得:
![]() ,可得:k=
,可得:k=![]() ,
,
∴反比例函数解析式:y=![]() (x>0);
(x>0);
(2)设OA=a(a>0),过点F作FM⊥x轴于M,
∵∠AOB=60°,
∴AH=![]() a,OH=
a,OH=![]() ,
,
∴S△AOH=![]() ,
,
∵S△AOF=![]() ,
,
∴S平行四边形AOBC=![]() ,
,
∵F为BC的中点,
∴S△OBF=![]() ,
,
∵BF=![]() a,∠FBM=∠AOB,
a,∠FBM=∠AOB,
∴FM=![]() ,BM=
,BM=![]() a,
a,
∴S△BMF=![]() BM*FM=
BM*FM=![]() ,
,
∴S△FOM=S△OBF+S△BMF=![]() ,
,
∵点A,F都在y=的图象上,
∴S△AOH=![]() k,
k,
∴![]() ,
,
∴a=![]() ,
,
∴OA=8![]() ,
,
∴AH=![]() ,OH=
,OH=![]() ,
,
∵S平行四边形AOBC=OB*AH=![]() ,
,
∴OB=![]() ,
,
∴C(![]() );
);
(3)存在三种情况:这样的P点有四个
当∠APO=90°时,在OA的两侧各有一点P,分别为:P1(![]() ),P2(
),P2(![]() ),
),
当∠PAO=90°时,P3(![]() ),
),
当∠POA=90°时,P4(![]() )
)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案