Question

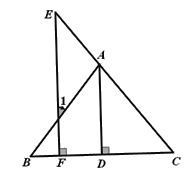
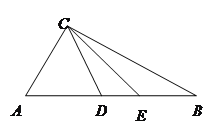
【题目】如图，在等边△ABC中，D是BC边的中点，以AD为边作等边△ADE．

(1)求∠CAE的度数；

(2)取AB边的中点F，连接CF、CE，试说明四边形AFCE是矩形．

Answer 1

【答案】（1）∠CAE=30°；（2）证明见解析.

【解析】分析：（1）根据等边三角形三线合一的特点，易求得∠DAC=30°，则∠CAE=∠DAE-∠DAC．
（2）先证明四边形AECF是平行四边形，然后根据∠CFA=∠FAE=90°，由矩形的定义判定四边形AFCE是矩形．

详解：

（1） ∵△ABC是等边三角形，且D是BC中点，

∴DA平分∠BAC，即∠DAB=∠DAC=30°；

∵△DAE是等边三角形，

∴∠DAE=60°；

∴∠CAE=∠DAE-∠CAD=30°；

（2）证明：∵△BAC是等边三角形，F是AB中点，

∴CF⊥AB；

∴∠BFC=90°,

由（1）知：∠CAE=30°，∠BAC=60°；

∴∠FAE=90°；

∴AE∥CF；

∵△BAC是等边三角形，且AD、CF分别是BC、AB边的中线，

∴AD=CF；

又AD=AE，∴CF=AE；

∴四边形AFCE是平行四边形；

∵∠AFC=∠FAE=90°，

∴四边形AFCE是矩形．