题目内容
【题目】如图，点P、Q是边长为2的菱形ABCD中两边BC和CD的中点，K是BD上一动点，则KP+KQ的最小值为________．
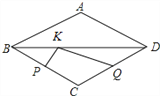
【答案】2
【解析】分析：先作点P关于BD的对称点P′，连接P′Q交BD于K，此时PK+QK有最小值．然后证明四边形BCQP′为平行四边形，即可求出PK+QK=P′Q=BC=2．
详解：
作点P关于BD的对称点P′，连接P′Q交BD于K，此时KP+KQ有最小值，最小值为P′Q的长．
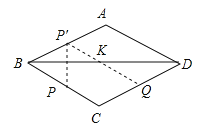
∵菱形ABCD关于BD对称，P是BC边上的中点，
∴P′是AB的中点，
又∵Q是CD边上的中点，
∴BP′∥CQ，BP′=CQ，
∴四边形BCQP′是平行四边形，
∴P′Q=BC=2，
∴PK+KQ=P′Q=2，即KP+KQ的最小值为2，
故答案为：2．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
【题目】今年，某市政府的一项实事工程就是由政府投入1 000万元资金，对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造，某社区为配合政府完成该项工作，对社区内1 200户家庭中的120户进行了随机抽样调查，并汇总成下表：
改造情况 | 均不改造 | ||||||
改造水龙头 | 改造马桶 | ||||||
1个 | 2个 | 3个 | 4个 | 1个 | 2个 | ||
户数 | 20 | 31 | 28 | 21 | 12 | 69 | 2 |
(1)试估计该社区需要对水龙头或马桶进行改造的家庭共有___户；
(2)改造后，一个水龙头一年大概可节约5吨水，一个马桶一年大约可节约15吨水，试估计该社区一年共可节约多少吨水？
(3)在抽样的120户家庭中，既要改造水龙头又要改造马桶的家庭共有多少户？
