题目内容
【题目】(1)如图![]() 示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
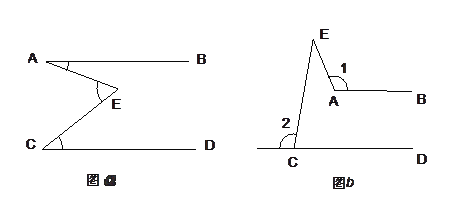
(2)现在如图b示,仍有AB∥CD,但点E在AB与CD的上方,①请尝试探索∠1,∠2,∠E三者的数量关系. ②请说明理由.
【答案】(1)证明见解析(2)∠1+∠2-∠E=180°
【解析】
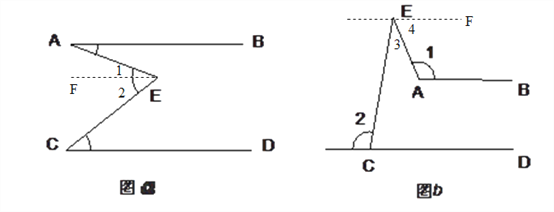
试题(1)过点E作EF∥AB,由两直线平行,内错角相等,得到∠A=∠1.
由平行的传递性得到EF // CD,再由平行线的性质得到∠2=∠C,由角的和差即可得到结论;
(2)过点E作EF∥AB,类似可得到结论.
试题解析:解:(1)过点E作EF∥AB,∴∠A=∠1(两直线平行,内错角相等).
∵AB // CD(已知),∴EF // CD(平行的传递性),∴∠2=∠C(两直线平行,内错角相等).
∵∠AEC=∠1+∠2(图上可知),∴∠AEC=∠A+∠C(等量代换) ;
(2)∠1+∠2-∠E=180°.理由如下:
过点E作EF∥AB,∴∠4+∠1=180°(两直线平行,同旁内角互补).
∵AB // CD(已知),∴EF // CD(平行的传递性),∴∠FEC=∠2(两直线平行,内错角相等),即∠3+∠4=∠2,∴∠4=∠2-∠3(等式性质),∴∠2-∠3+∠1=180°(等量代换),
即∠1+∠2-∠AEC=180°.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案【题目】今年,某市政府的一项实事工程就是由政府投入1 000万元资金,对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造,某社区为配合政府完成该项工作,对社区内1 200户家庭中的120户进行了随机抽样调查,并汇总成下表:
改造情况 | 均不改造 | ||||||
改造水龙头 | 改造马桶 | ||||||
1个 | 2个 | 3个 | 4个 | 1个 | 2个 | ||
户数 | 20 | 31 | 28 | 21 | 12 | 69 | 2 |
(1)试估计该社区需要对水龙头或马桶进行改造的家庭共有___户;
(2)改造后,一个水龙头一年大概可节约5吨水,一个马桶一年大约可节约15吨水,试估计该社区一年共可节约多少吨水?
(3)在抽样的120户家庭中,既要改造水龙头又要改造马桶的家庭共有多少户?