题目内容
【题目】已知正比例函数y=k1x的图象与反比例函数y= ![]() 的图象的一个交点是(2,3).
的图象的一个交点是(2,3).
(1)求出这两个函数的表达式;
(2)作出两个函数的草图,利用你所作的图形,猜想并验证这两个函数图象的另一个交点的坐标;
(3)直接写出使反比例函数值大于正比例函数值的x的取值范围.
【答案】
(1)解:由正比例函数y=k1x的图象与反比例函数y= ![]() 的图象的一个交点是(2,3),得
的图象的一个交点是(2,3),得
3=2k1,3= ![]() .
.
解得k1= ![]() ,k2=6.
,k2=6.
正比例函数y= ![]() x;反比例函数y=
x;反比例函数y= ![]()
(2)解:画出函数的图象如图:
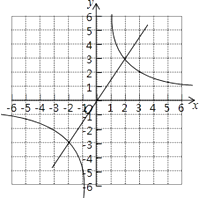
两个函数图象的一个交点的坐标(2,3),猜想另一个交点的坐标(﹣2,﹣3),
把(﹣2,﹣3)代入y= ![]() 成立
成立
(3)解:由图象可知:比例函数值大于正比例函数值的x的取值范围是x<﹣2或0<x<2
【解析】(1)根据待定系数法,可得函数解析式;(2)根据函数解析式确定出图象所经过的点的坐标,再画出图象即可.(3)根据图象和交点坐标即可求得.

练习册系列答案
相关题目