题目内容
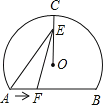
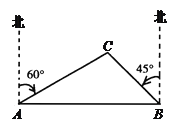
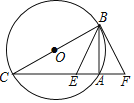
【题目】如图,BC为圆O直径,BF与圆O相切于点B,CF交圆O于A,E为AC上一点,使∠EBA=∠FBA,若EF=6,tan∠F=![]() ,则CE的长为_____.
,则CE的长为_____.
【答案】5![]()
【解析】
根据切线的性质和圆周角定理得出∠BAC=90°=∠BAF=∠FBC,根据全等三角形的判定得出△BAE≌△BAF,求出BE=BF,AE=AF,求出AE=AF=3,BF=BE=5,根据相似三角形的判定得出△FAB∽△FBC,根据相似三角形的性质得出比例式,求出FC长,即可得出答案.
解:∵BC为圆O直径,BF与圆O相切于点B,
∴∠BAC=90°=∠BAF=∠FBC,
在△BAE和△BAF中
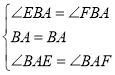
∴△BAE≌△BAF(ASA),
∴BE=BF,AE=AF,
∵EF=6,tan∠F=![]() =
=![]() ,
,
∴AE=AF=3,AB=5,
由勾股定理得:BF=![]() =
=![]() ,
,
∵∠BAF=∠FBC,∠F=∠F,
∴△FAB∽△FBC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:FC=![]() ,
,
∵AE=AF=3,
∴CE=![]() ﹣3﹣3=
﹣3﹣3=![]() ,
,
故答案为:5![]() .
.

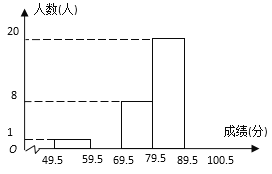
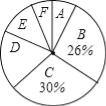
【题目】为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
分组 | 家庭用水量x/吨 | 家庭数/户 |
A | 0≤x≤4.0 | 4 |
B | 4.0<x≤6.5 | 13 |
C | 6.5<x≤9.0 | |
D | 9.0<x≤11.5 | |
E | 11.5<x≤14.0 | 6 |
F | x>4.0 | 3 |
根据以上信息,解答下列问题
(1)家庭用水量在4.0<x≤6.5范围内的家庭有 户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是 %;
(2)本次调查的家庭数为 户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是 %;
(3)家庭用水量的中位数落在 组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
【题目】科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一段时间后,记录下这种植物高度的增长情况(如下表):
温度x/℃ | … | ﹣4 | ﹣2 | 0 | 2 | 4 | 6 | … |
植物每天高度的增长量y/mm | … | 41 | 49 | 49 | 41 | 25 | 1 | … |
由这些数据,科学家推测出植物每天高度的增长量y是温度x的二次函数,那么下列三个结论:
①该植物在0℃时,每天高度的增长量最大;
②该植物在﹣6℃时,每天高度的增长量能保持在25mm左右;
③该植物与大多数植物不同,6℃以上的环境下高度几乎不增长.
上述结论中,所有正确结论的序号是
A. ①②③ B. ①③ C. ①② D. ②③