题目内容
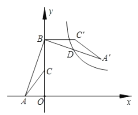
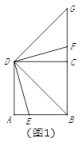
【题目】⑴如图1,![]() 是正方形
是正方形![]() 边
边![]() 上的一点,连接
上的一点,连接![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转90°,旋转后角的两边分别与射线
逆时针旋转90°,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .
.
①线段![]() 和
和![]() 的数量关系是 ;
的数量关系是 ;
②写出线段![]() 和
和![]() 之间的数量关系.
之间的数量关系.
⑵当四边形![]() 为菱形,
为菱形,![]() ,点
,点![]() 是菱形
是菱形![]() 边
边![]() 所在直线上的一点,连接
所在直线上的一点,连接![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转120°,旋转后角的两边分别与射线
逆时针旋转120°,旋转后角的两边分别与射线![]() 交于点
交于点![]() 和点
和点![]() .
.
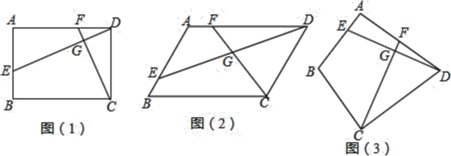
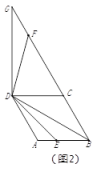
①如图2,点![]() 在线段上时,请探究线段
在线段上时,请探究线段![]() 和
和![]() 之间的数量关系,写出结论并给出证明;
之间的数量关系,写出结论并给出证明;
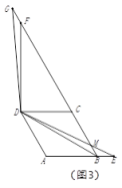
②如图3,点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 交射线
交射线![]() 于点
于点![]() ;若
;若 ![]() ,直接写出线段
,直接写出线段![]() 的长度.
的长度.
【答案】⑴①![]() ; ②
; ②![]() ;⑵①
;⑵①![]() . 理由见解析,②
. 理由见解析,②![]() 的长度为
的长度为![]() . 理由见解析.
. 理由见解析.
【解析】
(1)①根据旋转的性质解答即可;
②根据正方形的性质和全等三角形的判定和性质解答即可;
(2)①根据菱形的性质和全等三角形的判定和性质解答即可;
②作辅助线,计算BD和BF的长,根据平行线分线段成比例定理可得BM的长,根据线段的差可得结论.
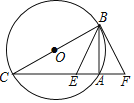
(1)①DB=DG,理由是:
∵∠DBE绕点B逆时针旋转90°,如图1,
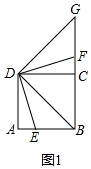
由旋转可知,∠BDE=∠FDG,∠BDG=90°,
∵四边形ABCD是正方形,
∴∠CBD=45°,
∴∠G=45°,
∴∠G=∠CBD=45°,
∴DB=DG;
故答案为:DB=DG;
②BF+BE=![]() BD,理由如下:
BD,理由如下:
由①知:∠FDG=∠EDB,∠G=∠DBE=45°,BD=DG,
∴△FDG≌△EDB(ASA),
∴BE=FG,
∴BF+FG=BF+BE=BC+CG,
Rt△DCG中,∵∠G=∠CDG=45°,
∴CD=CG=CB,
∵DG=BD=![]() BC,
BC,
即BF+BE=2BC=![]() BD;
BD;
(2)①如图2,BF+BE=![]() BD,
BD,
理由如下:在菱形ABCD中,∠ADB=∠CDB=![]() ∠ADC=
∠ADC=![]() ×60°=30°,
×60°=30°,
由旋转120°得∠EDF=∠BDG=120°,∠EDB=∠FDG,
在△DBG中,∠G=180°-120°-30°=30°,
∴∠DBG=∠G=30°,
∴DB=DG,
∴△EDB≌△FDG(ASA),
∴BE=FG,
∴BF+BE=BF+FG=BG,
过点D作DM⊥BG于点M,如图2,
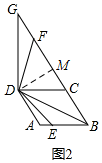
∵BD=DG,
∴BG=2BM,
在Rt△BMD中,∠DBM=30°,
∴BD=2DM.
设DM=a,则BD=2a,
DM=![]() a,
a,
∴BG=2![]() a,
a,
∴![]() ,
,
∴BG=![]() BD,
BD,
∴BF+BE=BG=![]() BD;
BD;
②过点A作AN⊥BD于N,过D作DP⊥BG于P,如图3,
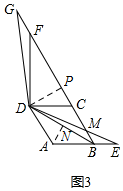
Rt△ABN中,∠ABN=30°,AB=2,
∴AN=1,BN=![]() ,
,
∴BD=2BN=2![]() ,
,
∵DC∥BE,
∴![]() ,
,
∵CM+BM=2,
∴BM=![]() ,
,
Rt△BDP中,∠DBP=30°,BD=2![]() ,
,
∴BP=3,
由旋转得:BD=BF,
∴BF=2BP=6,
∴GM=BG-BM=6+1-![]() =
=![]() .
.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
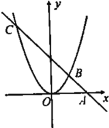
芒果教辅达标测试卷系列答案【题目】已知一个二次函数图象上部分点的横坐标![]() 与纵坐标
与纵坐标![]() 的对应值如表所示:
的对应值如表所示:
| … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
| … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
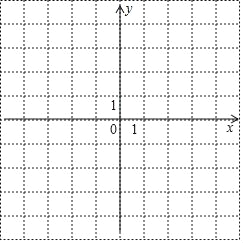
(1)求这个二次函数的表达式;
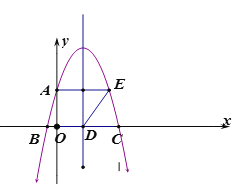
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
(3)当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.