题目内容
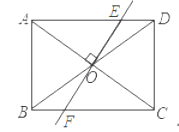
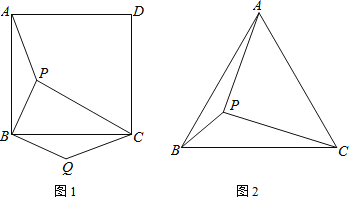
【题目】(1)如图1,点P是正方形ABCD内的一点,把△ABP绕点B顺时针方向旋转,使点A与点C重合,点P的对应点是Q.若PA=3,PB=2![]() ,PC=5,求∠BQC的度数.
,PC=5,求∠BQC的度数.
(2)点P是等边三角形ABC内的一点,若PA=12,PB=5,PC=13,求∠BPA的度数.
【答案】(1)135°;(2)150°
【解析】
(1)根据题意得出△ABP绕点B顺时针方向旋转了90°,才使点A与C重合,进而得出∠PBQ=90°,再利用勾股定理得出∠PQC的度数,进而求出∠BQC的度数;
(2)将△ABP绕点B顺时针方向旋转60°得到△CBP',由旋转知,△APB≌△CP'B,即∠BPA=∠BP'C,P'B=PB=5,P'C=PA=12,进而得出△PBP'也是正三角形,即∠PP'B=60°,PP'=5.
在△PP'C中,由勾股定理的逆定理得出∠PP'C=90°,从而可以得出结论.
(1)连接PQ.
由旋转可知:![]() ,QC=PA=3.
,QC=PA=3.
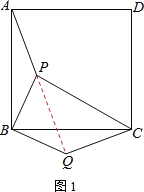
又∵ABCD是正方形,
∴△ABP绕点B顺时针方向旋转了90°,才使点A与C重合,
即∠PBQ=90°,∴∠PQB=45°,PQ=4.
则在△PQC中,PQ=4,QC=3,PC=5,∴PC2=PQ2+QC2.
即∠PQC=90°.
故∠BQC=90°+45°=135°.
(2)将△ABP绕点B顺时针方向旋转60°得到△CBP',
此时点P的对应点是点P'.
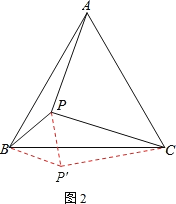
由旋转知,△APB≌△CP'B,即∠BPA=∠BP'C,P'B=PB=5,P'C=PA=12.
又∵△ABC是正三角形,∴∠ABP+∠PBC=60°,
∴∠CBP'+∠PBC=60°,∴∠PBP'=60°.
又∵P'B=PB=5,∴△PBP'也是正三角形,即∠PP'B=60°,PP'=5.
在△PP'C中,∵PC=13,PP'=5,P'C=12,∴PC2=PP'2+P'C2.
即∠PP'C=90°.
故∠BPA=∠BP'C=60°+90°=150°.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案【题目】已知y=ax2+bx+c(其中a,b,c为常数,且a≠0),乐老师在用描点法画其的图象时,列出如下表格,根据该表格,下列判断中不正确的是( )
x | … | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣2 | 2.5 | 4 | 2.5 | … |
A. a<0
B. 一元二次方程ax2+bx+c﹣5=0没有实数根
C. 当x=3时y=﹣2
D. 一元二次方程ax2+bx+c=0有一根比3大