ћвƒњƒЏ»Ё
°Њћвƒњ°њƒ≥–£ќ™ЅЋЅЋљв—І…ъґ‘ ј≤©јс“«µƒ÷™ѕю≥ћґ»£ђі”»Ђ–£1200√ы—І…ъ÷–Ћжїъ≥й»°ЅЋ50√ы—І…ъљш––≤в ‘£ЃЄщЊЁ≤в ‘≥…Љ®£®≥…Љ®»°’ы э£ђ¬ъЈ÷ќ™100Ј÷£©„чЅЋЌ≥Љ∆Ј÷ќц£ђїж÷∆≥…∆µ эЈ÷≤Љ÷±ЈљЌЉ£®»зЌЉ£ђ∆д÷–≤њЈ÷ эЊЁ»± І£©£Ѓ”÷÷™90Ј÷“‘…ѕ£®Їђ90Ј÷£©µƒ»Ћ э±»60~70Ј÷£®Їђ60Ј÷£ђ≤їЇђ70Ј÷£©µƒ»Ћ эµƒ2±ґїєґа3»Ћ£Ѓ«лƒгЄщЊЁ…ѕ ц–≈ѕҐ£ђљвірѕ¬Ѕ–ќ ћв£Ї
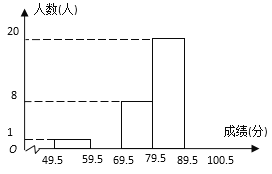
£®1£©Є√Ќ≥Љ∆Ј÷ќцµƒ—щ±Њ «£® £©
A.1200√ы—І…ъ£ї
B.±ї≥й»°µƒ50√ы—І…ъ£ї
C.±ї≥й»°µƒ50√ы—І…ъµƒќ Њн≥…Љ®£ї
D.50
£®2£©±ї≤в—І…ъ÷–£ђ≥…Љ®≤їµЌ”Џ90Ј÷µƒ”–ґа…ў»Ћ£њ
£®3£©≤в ‘≥…Љ®µƒ÷–ќї эЋщ‘ЏµƒЈґќІ « £ї
£®4£©»зєы∞—≤в ‘≥…Љ®≤їµЌ”Џ80Ј÷Љ«ќ™”≈ЅЉ£ђ ‘єјЉ∆Є√–£”–ґа…ў√ы—І…ъґ‘ ј≤©јс“«µƒ÷™ѕю≥ћґ»іпµљ”≈ЅЉ£ї
£®5£©—І–£„Љ±Єі”’в50√ы—І…ъ÷–£ђ“‘≤в ‘≥…Љ®≤їµЌ”Џ90Ј÷ќ™±к„Љ£ђЋжїъ—°3»Ћ“еќс–ыіЂ ј≤©јс“«£ђ»ф–°љ№µƒµ√Ј÷ «93Ј÷£ђƒ«√і–°љ№±ї—°…ѕµƒЄ≈¬ «ґа…ў£њ
°Њір∞Є°њ£®1£©C£ї£®2£©15£ї£®3£©79.5°™89.5£ї£®4£©840£ї£®5£©![]()
°Њљвќц°њ
£®1£©ЄщЊЁ—щ±Њµƒґ®“е£ђЄ√Ќ≥Љ∆Ј÷ќцµƒ—щ±Њ «±ї≥й»°µƒ50√ы—І…ъµƒ≤в ‘≥…Љ®.
£®2£©њ…“‘…и60°™°™70Ј÷£®Їђ60Ј÷£ђ≤їЇђ70Ј÷£©µƒ»Ћ эќ™![]() »Ћ£ђ‘т90Ј÷“‘…ѕ£®Їђ90Ј÷£©µƒ»Ћ эќ™
»Ћ£ђ‘т90Ј÷“‘…ѕ£®Їђ90Ј÷£©µƒ»Ћ эќ™![]() £ђЄщЊЁћвƒњ÷–µƒ эЅњєЎѕµЅ–≥ц“ї‘™“їіќЈљ≥ћљвірЉіњ….
£ђЄщЊЁћвƒњ÷–µƒ эЅњєЎѕµЅ–≥ц“ї‘™“їіќЈљ≥ћљвірЉіњ….
£®3£©ЄщЊЁ÷–ќї эµƒґ®“е—∞’“∆дЋщ‘Џµƒ≥…Љ®«шЉдЉіњ….
£®4£©ЄщЊЁ—щ±Њ«йњцЉ∆Ћг≥ц≥…Љ®”≈ЅЉµƒ—І…ъ»Ћ эЋщ’Љ±»јэ£ђ‘ў≥Ћ“‘Є√–£—І…ъ„№»Ћ эЉіњ….
£®5£©”…µЏ£®2£©ќ њ…÷™£ђ90Ј÷“‘…ѕ£®Їђ90Ј÷£©µƒ»Ћ эќ™15»Ћ£ђ∞і’’—°»Ћєж‘т–°љ№”–3іќїъїб£ђ‘тЄ≈¬ ќ™![]() £ђїѓЉтЉіњ….
£ђїѓЉтЉіњ….
£®1£©C£ї
£®2£©љв£Ї…и60°™°™70Ј÷£®Їђ60Ј÷£ђ≤їЇђ70Ј÷£©µƒ»Ћ эќ™![]() »Ћ£ђ‘т90Ј÷“‘…ѕ£®Їђ90Ј÷£©µƒ»Ћ эќ™
»Ћ£ђ‘т90Ј÷“‘…ѕ£®Їђ90Ј÷£©µƒ»Ћ эќ™![]() £ђ
£ђ
”…ћв“вњ…µ√![]()
љвµ√![]() £ђ
£ђ
![]() .
.
Ћщ“‘≥…Љ®≤їµЌ”Џ90Ј÷µƒ”–15»Ћ.
£®3£©79.5°™89.5
£®4£©![]() »Ћ,є єјЉ∆Є√–£”–840√ы—І…ъґ‘ ј≤©јс“«µƒ÷™ѕю≥ћґ»іпµљ”≈ЅЉ.
»Ћ,є єјЉ∆Є√–£”–840√ы—І…ъґ‘ ј≤©јс“«µƒ÷™ѕю≥ћґ»іпµљ”≈ЅЉ.
£®5£©![]() .
.
є –°љ№±ї—°…ѕµƒЄ≈¬ «![]() .
.

°Њћвƒњ°њƒ≥≤њ√≈ќ™–¬µƒ…ъ≤ъѕя—–ЈҐЅЋ“їњоїъ∆ч»Ћ£ђќ™ЅЋЅЋљвЋьµƒ≤ў„чЉЉƒ№«йњц£ђ‘ЏѕаЌђћхЉюѕ¬”л»Ћє§≤ў„чљш––ЅЋ≥й—щґ‘±»£Ѓєэ≥ћ»зѕ¬£ђ«л≤є≥дЌк’ы£Ѓ
’Љѓ эЊЁґ‘Ќђ“їЄц…ъ≤ъґѓ„ч£ђїъ∆ч»ЋЇЌ»Ћє§Єч≤ў„ч20іќ£ђ≤в ‘≥…Љ®£® ЃЈ÷÷∆£©»зѕ¬£Ї
їъ∆ч»Ћ | 8.0 | 8.1 | 8.1 | 8.1 | 8.2 | 8.2 | 8.3 | 8.4 | 8.4 | 9.0 |
9.0 | 9.0 | 9.1 | 9.1 | 9.4 | 9.5 | 9.5 | 9.5 | 9.5 | 9.6 | |
»Ћє§ | 6.1 | 6.2 | 6.6 | 7.2 | 7.2 | 7.5 | 8.0 | 8.2 | 8.3 | 8.5 |
9.1 | 9.6 | 9.8 | 9.9 | 9.9 | 9.9 | 10 | 10 | 10 | 10 |
’ыјн°Ґ√и ц эЊЁ∞і»зѕ¬Ј÷ґќ’ыјн°Ґ√и ц’вЅљ„й—щ±Њ эЊЁ£Ї
≥…Љ®x »Ћ э …ъ≤ъЈљ љ | 6°№x£Љ7 | 7°№x£Љ8 | 8°№x£Љ9 | 9°№x°№10 |
їъ∆ч»Ћ | 0 | 0 | 9 | 11 |
»Ћє§ | °° °° | °° °° | °° °° |
£®Ћµ√ч£Ї≥…Љ®‘Џ9.0Ј÷Љ∞“‘…ѕќ™≤ў„чЉЉƒ№”≈–г£ђ8.0°Ђ8.9Ј÷ќ™≤ў„чЉЉƒ№ЅЉЇ√£ђ6.0°Ђ7.9Ј÷ќ™≤ў„чЉЉƒ№ЇѕЄс£ђ6.0Ј÷“‘ѕ¬ќ™≤ў„чЉЉƒ№≤їЇѕЄс£©
Ј÷ќц эЊЁЅљ„й—щ±Њ эЊЁµƒ∆љЊщ э°Ґ÷–ќї э°Ґ÷Џ эЇЌЈљ≤о»зѕ¬±нЋщ Њ£Ї
∆љЊщ э | ÷–ќї э | ÷Џ э | Јљ≤о | |
їъ∆ч»Ћ | 8.8 | °°9.0°° | 9.5 | 0.333 |
»Ћє§ | 8.6 | °°8.8°° | 10 | 1.868 |
µ√≥цљб¬џ
£®1£©»зєы…ъ≤ъ≥ц“їЄц≤ъ∆Ј£ђ–и“™Ќк≥…Ќђ—щµƒ≤ў„ч200іќ£ђєјЉ∆їъ∆ч»Ћ…ъ≤ъ’вЄц≤ъ∆Јіпµљ≤ў„чЉЉƒ№”≈–гµƒіќ эќ™°° °°£ї
£®2£©«лљбЇѕ эЊЁЈ÷ќцїъ∆ч»ЋЇЌ»Ћє§‘Џ≤ў„чЉЉƒ№Јљ√жЄч„‘µƒ”≈ ∆£Ї°° °°£Ѓ