Question

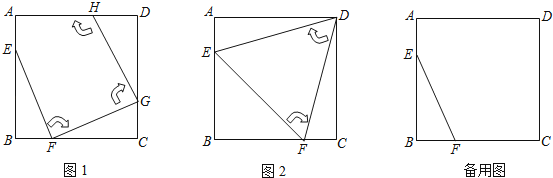
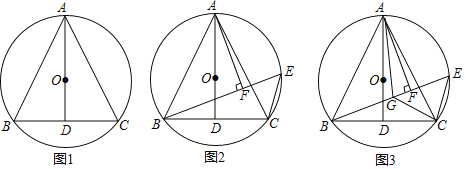
【题目】如图1，△ABC内接于圆O，连接AO，延长AO交BC于点D，AD⊥BC．

（1）求证：AB＝AC；

（2）如图2，在圆O上取一点E，连接BE、CE，过点A作AF⊥BE于点F，求证：EF+CE＝BF；

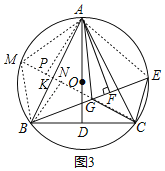
（3）如图3在（2）的条件下，在BE上取一点G，连接AG、CG，若∠AGB+∠ABC＝90°，∠AGC＝∠BGC，AG＝6，BG＝5，求EF的长．

Answer 1

【答案】（1）见解析；（2）见解析；（3）EF=．

【解析】

（1）由垂径定理可得BD＝CD，由垂直平分线的性质可得AB＝AC；

（2）在BF上截取FH＝EF，连接AE，由“SAS”可证△ABH≌△ACE，可得BH＝CE，可得结论；

（3）延长CG交圆O于M，交AB于K，过点A作AP⊥CM于P，过点B作BN⊥CM于N，连接AE，通过等腰三角形的性质和相似三角形的性质，分别求出BF，CE的长，即可求EF的长．

证明：（1）∵AD⊥BC，AD过圆心O，

∴BD＝CD，且AD⊥BC，

∴AB＝AC；

（2）如图2，在BF上截取FH＝EF，连接AE，AH，

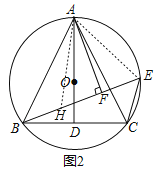
∵AF⊥EH，EF＝FH，

∴AH＝AE，

∴∠AHE＝∠AEH，

∵AB＝AC，

∴∠ABC＝∠ACB，且∠ACB＝∠AEH，

∴∠AEH＝∠AHE＝∠ABC＝∠ACB，

∴∠BAC＝∠HAE，

∴∠BAH＝∠CAE，且AH＝AE，AB＝AC，

∴△ABH≌△ACE（SAS）

∴BH＝CE，

∴BF＝EF+CE；

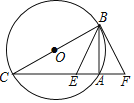
（3）如图3，延长CG交⊙O于M，交AB于K，过点A作AP⊥CM于P，过点B作BN⊥CM于N，连接AE，AM，MB，

∵∠AGB+∠ABC＝90°，

∴∠AGB＝90°﹣∠ABC，

∴∠AGB＝2∠BAC，

∵∠AGC＝∠BGC，

∴∠BGM＝∠AGM＝∠AGB，

∴∠BGM＝∠AGM＝∠BAC，且∠BAC＝∠BMC，

∴∠BMG＝∠BGM，

∴BM＝BG＝5，

∵∠AMC＝∠ABC，∠AGM＝∠BAC，

∴∠GAM＝∠ACB，

∴∠AMG＝∠MAG，

∴MG＝AG＝6，

∵BM＝BG，BN⊥MG，

∴MN＝NG＝3，

∴BN＝＝＝4，

∵∠BMG＝∠AGM，

∴BM∥AG，

∴，

∵AP∥BN，

∴，

∴AP＝，

∴PG＝，

∴PN＝PG﹣NG＝，且

∴PK＝，KN＝，

∴AK＝，

BK＝，

∴AB＝AK+BK＝，

∵AF2＝AG2﹣GF2，AF2＝AB2﹣BF2，

∴AG2﹣GF2＝AB2﹣（5+GF）2，

∴GF＝，

∴BF＝，

∵MP＝MG﹣PG＝，

∴MK＝，

∵∠AMC＝∠ABC，∠MAB＝∠BCM，

∴△MAK∽△BCK，

∴，

∴CK＝，

∴GC﹣KC﹣KG＝，

∵∠BMC＝∠BEC，∠BGM＝∠CGE，∠BGM＝∠BMG，

∴∠CGE＝∠CEG，

∴CG＝CE＝，

∵EF+CE＝BF，

∴EF＝BF﹣CE＝．