Question

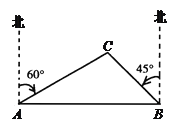
【题目】已知：如图，一艘渔船正在港口A的正东方向40海里的B处进行捕鱼作业，突然接到通知，要该船前往C岛运送一批物资到A港，已知C岛在A港的北偏东60°方向，且在B的北偏西45°方向．问该船从B处出发，以平均每小时20海里的速度行驶，需要多少时间才能把这批物资送到A港(精确到1小时)（该船在C岛停留半个小时）?（，，）

Answer 1

【答案】3小时.

【解析】

作CD⊥AB于D点．设CD=x海里，在直角△ACD中，利用x表示出AC，AD，同理表示出BD，BC，根据AB=40即可列出方程求得CD的长，则AC+CB即可求得，然后除以速度即可得到时间．

作CD⊥AB于D点．设CD=x海里，

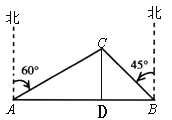
在直角△ACD中，∠CAD=90°-60°=30°，

则AC=2x，AD=x，

在直角△BCD中，∠CBD=45°，

则BD=CD=x，BC=CD=x，

∵AB=40，即AD+BD=40，

∴x+x=40，

解得：x=20（-1），

∴BC=20（-1）=20-20，AC=2x=40（-1），

则总路程是：20-20+40（-1）海里，

则时间是：（小时）．

∵该船在C岛停留半个小时，

∴需要3小时能把这批物资送到A港．

考点: 解直角三角形的应用-方向角问题.