Question

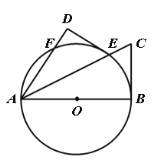
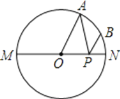
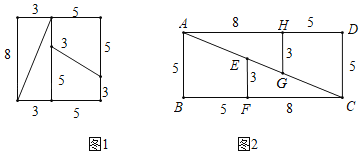
【题目】直觉的误差：有一张8cm×8cm的正方形纸片，面积是64cm2．把这些纸片按图1所示剪开成四小块，其中两块是三角形，另外两块是梯形．把剪出的4个小块按图2所示重新拼合，这样就得到了一个13cm×5cm的长方形，面积是65cm2，面积多了1cm2，这是为什么？

小明给出如下证明：如图2，可知，tan∠CEF＝，tan∠EAB＝，∵tan∠CEF＞tan∠EAB，∴∠CEF＞∠EAB，∵EF∥AB，∴∠EAB+∠AEF＝180°，∴CEF+∠AEF＞180°，因此A、E、C三点不共线．同理A、G、C三点不共线，所以拼合的长方形内部有空隙，故面积多了1cm2

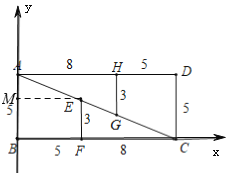
（1）小红给出的证明思路为：以B为原点，BC所在的直线为x轴，建立平面直角坐标系，证明三点不共线．请你帮小红完成她的证明；

（2）将13cmx13cm的正方形按上述方法剪开拼合，是否可以拼合成一个长方形，但面积少了1cm2？如果能，求出剪开的三角形的短边长；如果不能，说明理由．

Answer 1

【答案】(1) 见解析；(2) 5cm

【解析】

(1)以B为原点，BC所在的直线为x轴，建立平面直角坐标系，在Rt△EFC中，求出EC的长，在直角梯形ABFE中，求出AE长，若A、E、C三点共线，则在Rt△ABC中，利用勾股定理求出AC长，比较AC与AE+EC的大小即可得出结论；

(2)设剪开的长方形短边长为xcm，根据题意可得关于x的方程，解方程即可求得答案.

(1)以B为原点，BC所在的直线为x轴，建立平面直角坐标系，

在Rt△EFC中，EC＝，

在直角梯形ABFE中，过点E作EM⊥AB，则四边形BFEM是矩形，

∴BM=EF=3，

∴AM=5-3=2，

∴AE＝，

若A、E、C三点共线，则在Rt△ABC中，

AC＝，

∵，

∴A、E、C三点共线不共线，

∴所以拼合的长方形内部有空隙；

(2)设剪开的长方形短边长为xcm，

根据题意可得：

(13﹣x)(13+13﹣x)＝13×13﹣1，

∴x2﹣39x+170＝0，

∴x＝5或x＝34(舍)，

∴可以拼成成一个长方形，但面积少了1cm2，剪开的三角形的短边长是5cm.