题目内容
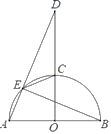
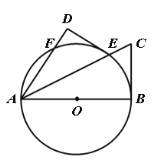
【题目】如图，已知AB是⊙O的直径，F是⊙O上一点，∠BAF的平分线交⊙O于点E，交⊙O的切线BC于点C，过点E作ED⊥AF，交AF的延长线于点D．
（1）求证：DE是⊙O的切线；
（2）若DE=3，CE=2，
①求
值；
②若点G 为AE上一点，求OG+
EG最小值．
【答案】（1）证明见解析（2）①
②3
【解析】
（1）作辅助线，连接OE．根据切线的判定定理，只需证DE⊥OE即可；
（2）①连接BE．根据BC、DE两切线的性质证明△ADE∽△BEC；又由角平分线的性质、等腰三角形的两个底角相等求得△ABE∽△AFD，所以
；
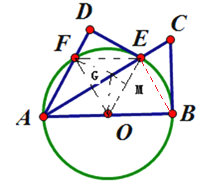
②连接OF，交AD于H，由①得∠FOE=∠FOA=60°,连接EF，则△AOF、△EOF都是等边三角形，故四边形AOEF是菱形，由对称性可知GO=GF,过点G作GM⊥OE于M，则GM=
EG，OG+EG=GF+GM,根据两点之间线段最短，当F、G、M三点共线，OG+EG=GF+GM=FM最小，此时FM =3.故OG+EG最小值是3.
（1）连接OE
∵OA=OE，∴∠AEO=∠EAO
∵∠FAE=∠EAO，∴∠FAE=∠AEO
∴OE∥AF
∵DE⊥AF，∴OE⊥DE
∴DE是⊙O的切线
（2）①解：连接BE
∵直径AB ∴∠AEB=90°
∵圆O与BC相切
∴∠ABC=90°
∵∠EAB+∠EBA=∠EBA+∠CBE=90°
∴∠EAB=∠CBE
∴∠DAE=∠CBE
∵∠ADE=∠BEC=90°
∴△ADE∽△BEC
∴
②连接OF，交AD于H，
由①，设BC=2x，则AE=3x
∵△BEC∽△ABC ∴
∴
解得：x1=2，
（不合题意，舍去）
∴AE=3x=6，BC=2x=4，AC=AE+CE=8
∴AB=
，∠BAC=30°
∴∠AEO=∠EAO=∠EAF=30°，∴∠FOE=2∠FAE=60°
∴∠FOE=∠FOA=60°,连接EF，则△AOF、△EOF都是等边三角形，∴四边形AOEF是菱形
由对称性可知GO=GF,过点G作GM⊥OE于M，则GM=EG，OG+EG=GF+GM,根据两点之间线段最短，当F、G、M三点共线，OG+EG=GF+GM=FM最小，此时FM=FOsin60o=3.
故OG+EG最小值是3.
