题目内容
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于A(2,﹣1)、B(
(x>0)的图象交于A(2,﹣1)、B(![]() ,n)两点.直线y=2与y轴交于点C.
,n)两点.直线y=2与y轴交于点C.
1)求一次函数与反比例函数的解析式;
2)求△ABC的面积;
3)直接写出不等式kx+b>![]() 在如图所示范围内的解集.
在如图所示范围内的解集.

【答案】(1)y=﹣![]() ;y=2x﹣5;(2)
;y=2x﹣5;(2)![]() ;(3)x<
;(3)x<![]() 或x>2
或x>2
【解析】分析:1)把A坐标代入反比例解析式求出m的值,确定出反比例解析式,再将B坐标代入求出n的值,确定出B坐标,将A与B坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;
2)利用两点间的距离公式求出AB的长,利用点到直线的距离公式求出点C到直线AB的距离,即可确定出三角形ABC面积.
3)根据函数图象,找到直线在双曲线上方部分对应的x的取值范围即可得.
详解:1)把A(2,﹣1)代入反比例解析式得:﹣1=![]() ,即m=﹣2,
,即m=﹣2,
∴反比例解析式为y=﹣![]() ,
,
把B(![]() ,n)代入反比例解析式得:n=﹣4,即B(
,n)代入反比例解析式得:n=﹣4,即B(![]() ﹣4),
﹣4),
把A与B坐标代入y=kx+b中得:![]() ,
,
解得:k=2,b=﹣5,
则一次函数解析式为y=2x﹣5;
2)如图,
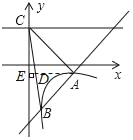
∵A(2,﹣1),B(![]() ,﹣4),直线AB解析式为y=2x﹣5,
,﹣4),直线AB解析式为y=2x﹣5,
∵C(0,2),直线BC解析式为y=﹣12x+2,
将y=﹣1代入BC的解析式得x=![]() ,则AD=2﹣
,则AD=2﹣![]() =
=![]()
∵xC﹣xB=2﹣(﹣4)=6,
∴S△ABC=![]() ×AD×(yC﹣yB)=
×AD×(yC﹣yB)=![]() ×
×![]() ×6=
×6=![]() .
.
3)由图可知,当x<![]() 或x>2时,kx+b>
或x>2时,kx+b>![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
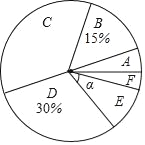
小学生10分钟应用题系列答案【题目】在星期一的第八节课,我校体育老师随机抽取了九年级的总分学生进行体育中考的模拟测试,并对成绩进行统计分析,绘制了频数分布表和统计图,按得分划分成A、B、C、D、E、F六个等级,并绘制成如下两幅不完整的统计图表.
等级 | 得分x(分) | 频数(人) |
A | 95<x≤100 | 4 |
B | 90<x≤95 | m |
C | 85<x≤90 | n |
D | 80<x≤85 | 24 |
E | 75<x≤80 | 8 |
F | 70<x≤75 | 4 |
请你根据图表中的信息完成下列问题:
1)本次抽样调查的样本容量是 .其中m= ,n= .
2)扇形统计图中,求E等级对应扇形的圆心角α的度数;
3)我校九年级共有700名学生,估计体育测试成绩在A、B两个等级的人数共有多少人?
4)我校决定从本次抽取的A等级学生(记为甲、乙、丙、丁)中,随机选择2名成为学校代表参加全市体能竞赛,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.