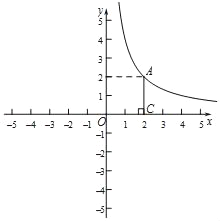
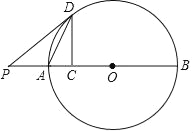
��Ŀ����
����Ŀ����ͼ��ʾ����֪������y��ax2��a��0����һ�κ���y��kx+b��ͼ���ཻ��A����1����1����B��2����4�����㣬��P���������ϲ���A��B�غϵ�һ�����㣬��Q��y���ϵ�һ�����㣮
��1����ֱ��д��a��k��b��ֵ������x�IJ���ʽax2��kx��2�Ľ⼯��
��2������P��ֱ��AB�Ϸ�ʱ���������PAB��������ֵ�������ʱ��P�����ꣻ
��3���Ƿ������P��Q��A��BΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д��P��Q�����ꣻ�������ڣ���˵�����ɣ�
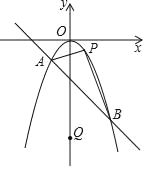
���𰸡���1��a����1��k����1��b����2��x����1��x��2����2����PAB��������ֵΪ![]() ����ʱ��P������Ϊ��
����ʱ��P������Ϊ��![]() ��
��![]() ������3��P����������3����9����3����9����1����1����Q��������Q��0����12����0����6����0����4����
������3��P����������3����9����3����9����1����1����Q��������Q��0����12����0����6����0����4����
��������
��1�����ô���ϵ�����������a��k��b��ֵ������ͼ�ɵó�����ʽ�Ľ⼯����2������A��y���ƽ���ߣ�����B��x���ƽ���ߣ����߽��ڵ�C������PC�����P�ĺ�����Ϊm�����P��������Ϊ��m2������P��PD��AC��D����PE��BC��E����D����1����m2����E��m����4�����ɴ˿ɵ�PD��m+1��PE����m2+4���ٸ���S��APB��S��APC+S��BPC��S��ABC���������ݼ��ɵ�S��APB��m�Ķ��κ�����ϵʽ�����ö��κ�������ֵ�ķ������m��ֵ��S��APB ��ֵ�������õ�P�����꼴�ɣ���3����3������ƽ���ı��ε����ʺ������ص��ɣ�
�⣺��1����A����1����1��������y��ax2�У��ɵã�a����1��
��A����1����1����B��2����4������y��kx+b�У��ɵã�![]() ��
��
��ã�![]() ��
��
����a����1��k����1��b����2��
����x�IJ���ʽax2��kx��2�Ľ⼯��x����1��x��2��
��2������A��y���ƽ���ߣ�����B��x���ƽ���ߣ����߽��ڵ�C��
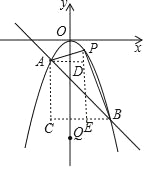
��A����1����1����B��2����4����
��C����1����4����AC��BC��3��
���P�ĺ�����Ϊm�����P��������Ϊ��m2��
����P��PD��AC��D����PE��BC��E����D����1����m2����E��m����4����
��PD��m+1��PE����m2+4��
��S��APB��S��APC+S��BPC��S��ABC
��![]()
��![]()
��![]() ��
��
��![]() ��0��
��0��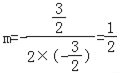 ����1��m��2��
����1��m��2��
�൱![]() ʱ��S��APB ��ֵ���
ʱ��S��APB ��ֵ���
�൱![]() ʱ��
ʱ��![]() ��S��APB��
��S��APB��![]() ��
��
����PAB��������ֵΪ![]() ����ʱ��P������Ϊ��
����ʱ��P������Ϊ��![]() ��
��![]() ��
��
��3������������������ĵ㣬
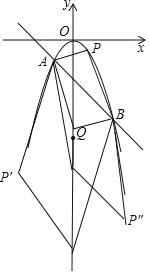
����P��Q��A��BΪ������ı�����ƽ���ı���ʱ��
��AP��BQ��AQ��BP��A����1����1����B��2����4����
�ɵ��������£�
��P��ĺ�����Ϊ��3��������κ�������ʽ��
��ã�P'����3����9����Q'��0����12����
��P��ĺ�����Ϊ3��������κ�������ʽ��
��ã�P�壨3����9����Q�壨0����6����
��P�ĺ�����Ϊ1��������κ�������ʽ��
��ã�P��1����1����Q��0����4����
�ʣ�P������Ϊ����3����9����3����9����1����1����
Q��������Q��0����12����0����6����0����4����