题目内容
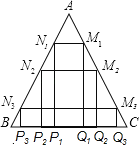
【题目】如图,在△ABC中,AB=AC=![]() ,BC=2.现分别任作△ABC的内接矩形P1Q1M1N1,P2Q2M2N2,P3Q3M3N3,设这三个内接矩形的周长分别为c1、c2,c3,则c1+c2+c3的值是( )
,BC=2.现分别任作△ABC的内接矩形P1Q1M1N1,P2Q2M2N2,P3Q3M3N3,设这三个内接矩形的周长分别为c1、c2,c3,则c1+c2+c3的值是( )
A. 6B. ![]() C. 12D.
C. 12D. ![]()
【答案】C
【解析】
首先过点A作AD⊥BC于D,由等腰三角形的性质,可得BD=CD=![]() BC=1,∠B=∠C,由勾股定理可求得AD的长,又可证得△BN1P1∽△BAD,利用相似三角形的对应边成比例,可证得N1P1=2BP1,又由△BP1N1≌△CQ1M1(AAS),BP1=CQ1,则可求得c1的值,同理可求得c2,c3的值,继而求得答案.
BC=1,∠B=∠C,由勾股定理可求得AD的长,又可证得△BN1P1∽△BAD,利用相似三角形的对应边成比例,可证得N1P1=2BP1,又由△BP1N1≌△CQ1M1(AAS),BP1=CQ1,则可求得c1的值,同理可求得c2,c3的值,继而求得答案.
过点A作AD⊥BC于D,
∵AB=AC=![]() ,BC=2,
,BC=2,
∴BD=CD=![]() BC=1,∠B=∠C,
BC=1,∠B=∠C,
∴![]()
∵四边形P1Q1M1N1是矩形,
∴P1Q1=M1N1,N1P1=M1Q1,N1P1⊥BC,
∴N1P1∥AD,
∴△BN1P1∽△BAD,
∴BP1:BD=N1P1:AD,
∴N1P1=2BP1,
在△BP1N1和△CQ1M1中,
∵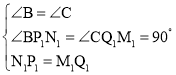
∴△BP1N1≌△CQ1M1(AAS),
∴BP1=CQ1,
∴c1=N1P1+P1Q1+M1Q1+M1N1=2BP1+2P1Q1+2BP1=2(BP1+P1Q1+BP1)=2(BP1+P1Q1+CQ1)=2BC=2×2=4,
同理:c2=c3=c1=4.
∴c1+c2+c3=12.
故选:C.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目