题目内容
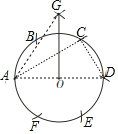
【题目】尺规作图特有的魅力使无数人沉湎其中.传说拿破仑曾通过下列尺规作图将圆等分:
①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;
②分别以点A,D为圆心,AC长为半径画弧,两弧相交于点G;
③连接OG,以OG长为半径,从点A开始,在圆周上依次截取,刚好将圆等分.顺次连接这些等分点构成的多边形面积为_____.

【答案】2r2
【解析】
根据作法得到六边形ABCDEF为⊙O的内接正六边形,则有∠CAD=30°,∠ACD=90°,利用特殊角的三角函数值得到CD=r,AC=![]() r,再利用作法得到GO⊥AD,利用勾股定理求得OG=
r,再利用作法得到GO⊥AD,利用勾股定理求得OG=![]() r,然后判断以OG长为半径,从点A 开始,在圆周上依次截取,刚好将圆4等分,顺次连接这些等分点构成了正方形,再利用正方形的面积公式进行计算即可.
r,然后判断以OG长为半径,从点A 开始,在圆周上依次截取,刚好将圆4等分,顺次连接这些等分点构成了正方形,再利用正方形的面积公式进行计算即可.
连接AD、AC、AG,如图,
∵将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点,
∴∠CAD=30°,∠ACD=90°,
∴CD=ADsin30°=r,AC=ADcos30°=![]() r,
r,
∵GA=GD,
∴GO⊥AD,
∴OG=![]() ,
,
以OG长为半径,从点A开始,在圆周上依次截取,刚好将圆4等分,顺次连接这些等分点构成的多边形为正方形,
∴这个多边形面积=![]() r
r![]() r=2r2,
r=2r2,
故答案为:2r2.

练习册系列答案
相关题目