题目内容
【题目】已知二次函数
（
）的图象与
轴交于不同的两点
，
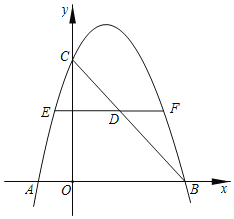
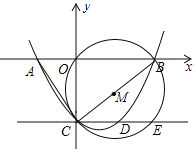
为二次函数图象的顶点．若
是边长为4的等边三角形，则
__________．
【答案】
【解析】
设点A、B的横坐标分别为m、n，利用根与系数的关系得：m+n=
，mn=
，根据AB=4=|m-n|，列式变形后得：b2-4ac=16a2，根据△ABC是边长为4的等边三角形，计算其高为
，即二次函数顶点的纵坐标为
，根据公式列式为
，可得结论．
解：设点A、B的横坐标分别为m、n，则m+n=，mn=，
∵AB=4=|m-n|，
∴（m-n）2=16，
∴m2-2mn+n2=（m+n）2-4mn=（）2-4×=16，
∴b2-4ac=16a2，
∵△ABC是边长为4的等边三角形，
∴点C到AB的距离为，
∵a＞0，
∴点C的纵坐标为，，
∴4ac-b2=
，
∴16a2=
，a=，
故答案为：.
练习册系列答案
相关题目
【题目】一汽车租赁公司拥有某种型号的汽车100辆．公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系：
x | 3000 | 3200 | 3500 | 4000 |
y | 100 | 96 | 90 | 80 |
（1）观察表格，用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y（辆）与每辆车的月租金x（元）之间的关系式.
（2）已知租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元．用含x（x≥3000）的代数式填表:
租出的车辆数 | 未租出的车辆数 | ||
租出每辆车的月收益 | 所有未租出的车辆每月的维护费 |
（3）若你是该公司的经理，你会将每辆车的月租金定为多少元，才能使公司获得最大月收益？请求出公司的最大月收益是多少元．
