题目内容
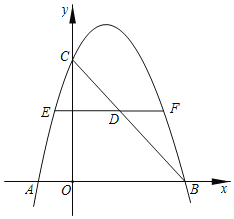
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+2x+a交x轴于点A,B,交y轴于点C,点A的横坐标为﹣2.
x2+2x+a交x轴于点A,B,交y轴于点C,点A的横坐标为﹣2.
(1)求抛物线的对称轴和函数表达式.
(2)连结BC线段,BC上有一点D,过点D作x轴的平行线交抛物线于点E,F,若EF=6,求点D的坐标.
【答案】(1)y=﹣![]() x2+2x+6;对称轴为x=2;(2)点D的坐标为(2.5,1.5).
x2+2x+6;对称轴为x=2;(2)点D的坐标为(2.5,1.5).
【解析】
(1)将点A的坐标代入函数的解析式求得a的值后即可确定二次的解析式,代入对称轴公式即可求得对称轴;
(2)首先根据点A的坐标和对称轴求得点B的坐标,然后求得直线BC的解析式,从而设出点D的坐标并表示出点EF的坐标,表示出EF的长后根据EF=6求解即可.
解:如图:
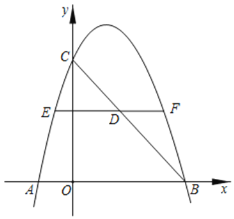
(1)∵A点的横坐标为﹣2,
∴A(﹣2,0),
∵点A 在抛物线y=﹣![]() x2+2x+a上,
x2+2x+a上,
∴﹣2﹣4+a=0,
解得:a=6,
∴函数的解析式为:y=﹣![]() x2+2x+6,
x2+2x+6,
∴对称轴为x=﹣![]() =﹣
=﹣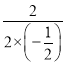 =2;
=2;
(2)∵A(﹣2,0),对称轴为x=2,
∴点B的坐标为(6,0),
∴直线BC的解析式为y=﹣x+6,
∵点D在BC上,
∴设点D的坐标为(m,﹣m+6),
∴点E和点F的纵坐标为﹣m+6,
∴y=﹣![]() x2+2x+6=﹣m+6,
x2+2x+6=﹣m+6,
解得:x=2±![]() ,
,
∴EF=2+![]() ﹣(2﹣
﹣(2﹣![]() )=2
)=2![]() ,
,
∵EF=6,
∴2![]() =6,
=6,
解得:m=2.5,
∴点D的坐标为(2.5,1.5).

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目