题目内容
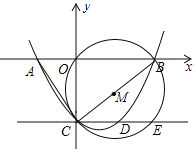
【题目】如图,抛物线y=ax2﹣![]() x+c与x轴相交于点A(﹣2,0)、B(4,0),与y轴相交于点C,连接AC,BC,以线段BC为直径作⊙M,过点C作直线CE∥AB,与抛物线和⊙M分别交于点D,E,点P在BC下方的抛物线上运动.
x+c与x轴相交于点A(﹣2,0)、B(4,0),与y轴相交于点C,连接AC,BC,以线段BC为直径作⊙M,过点C作直线CE∥AB,与抛物线和⊙M分别交于点D,E,点P在BC下方的抛物线上运动.
(1)求该抛物线的解析式;
(2)当△PDE是以DE为底边的等腰三角形时,求点P的坐标;
(3)当四边形ACPB的面积最大时,求点P的坐标并求出最大值.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣3;(2)P(3,﹣
x﹣3;(2)P(3,﹣![]() );(3)点P(2,﹣3),最大值为12
);(3)点P(2,﹣3),最大值为12
【解析】
(1)用交点式设出抛物线的表达式,化为一般形式,根据系数之间的对应关系即可求解;
(2)根据(1)中的表达式求出点C(0,-3),函数对称轴为:x=1,则点D(2,-3),点E(4,-3),当△PDE是以DE为底边的等腰三角形时,点P在线段DE的中垂线上,据此即可求解;
(3)求出直线BC的表达式,设出P、H点的坐标,根据四边形ACPB的面积=S△ABC+S△BHP+S△CHP进行计算,化为顶点式即可求解.
(1)抛物线的表达式为:y=a(x+2)(x﹣4)=a(x2﹣2x﹣8),
即﹣2a=﹣![]() ,解得:a=
,解得:a=![]() ,
,
故抛物线的表达式为:y=![]() x2﹣
x2﹣![]() x﹣3;
x﹣3;
(2)当x=0时,y=-3,故点C的坐标为(0,﹣3),
函数对称轴为:x=![]() =1,
=1,
∵CE∥AB
∴点D(2,﹣3),点E(4,﹣3),
则DE的中垂线为:x=![]() =3,
=3,
当x=3时,y=![]() x2﹣
x2﹣![]() x﹣3=﹣
x﹣3=﹣![]() ,
,
故点P(3,﹣![]() );
);
(3)设直线BC的解析式为y=kx+b,
把B(4,0)C(0,﹣3)代入得:![]()
解得: 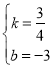
∴直线BC的表达式为:y=![]() x﹣3,
x﹣3,
故点P作y轴的平行线交BC于点H,
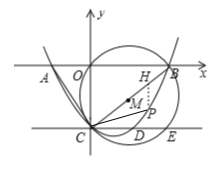
设点P(x,![]() x2﹣
x2﹣![]() x﹣3),则点H(x,
x﹣3),则点H(x,![]() x﹣3);
x﹣3);
四边形ACPB的面积=S△ABC+S△BHP+S△CHP=![]() 3×6+
3×6+![]() HP×OB=9+
HP×OB=9+![]() ×4×(
×4×(![]() x﹣3﹣
x﹣3﹣![]() x2+
x2+![]() x+3)=﹣
x+3)=﹣![]() x2+3x+9=
x2+3x+9=![]() ,
,
∵﹣![]() <0,故四边形ACPB的面积有最大值为12,此时,点P(2,﹣3).
<0,故四边形ACPB的面积有最大值为12,此时,点P(2,﹣3).