��Ŀ����
����Ŀ���������¹涨������ƽ��ֱ������ϵxOy�е�ͼ��M��N���������¶��壺PΪͼ��M������һ�㣬QΪN����һ�㣬���P��Q�����ľ��������Сֵʱ���ͳƸ���СֵΪ����ͼ��M��N֮��ġ��վ��롱�����P��Q�����ľ���������ֵʱ���ͳƸ����ֵΪ����ͼ��M��N֮��ġ������롱��
������ѧϰ��������������Ļ����ϣ�����������⣺
��ƽ��ֱ������ϵxOy�У���A����6��8����B����6����8����C��6����8����D��6��8����
��1������ƽ��ֱ������ϵ�л����ı���ABCD���߶�AB���߶�CD�ġ��վ��롱Ϊ�� �����������롱Ϊ�� ����
��2����ֱ��y����![]() x+b��b��0����x�ᣬy��ֱ��ڵ�E��F�����߶�EF���ı���ABCD�ġ��վ��롱��2�������ǵġ������롱��
x+b��b��0����x�ᣬy��ֱ��ڵ�E��F�����߶�EF���ı���ABCD�ġ��վ��롱��2�������ǵġ������롱��
��3����M��Բ��ΪM��m����6�����뾶Ϊ1������M���ABC�ġ��վ��롱����1��ֱ��д��m��ȡֵ��Χ��
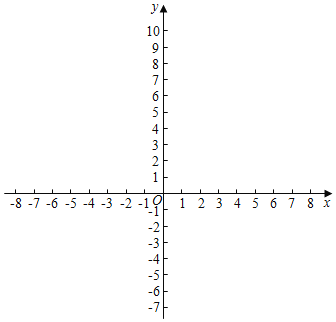
���𰸡���1��12��20����2��2![]() ��2
��2![]() ��2
��2![]() ����3����m����8��6+
����3����m����8��6+![]() ��4��m��6��3
��4��m��6��3![]() ʱ����M���ABC�ġ��վ��롱����1��
ʱ����M���ABC�ġ��վ��롱����1��
��������
��1���ɵ�����껭��ͼ�Σ��ɡ��վ��롱�͡������롱�Ķ������⣻
��2��������������ۣ������E����F���꣬���ɽ⣻
��3���ֵ�M��y�������Ҳ����ۣ��ҵ�����㣬������⣮
�⣺��1����ͼ��ʾ��

���߶�AB���߶�CD�ġ��վ��롱Ϊ12���������롱��![]() ��
��
�ʴ�Ϊ��12��20��
��2�����߶�EF���ı���ABCD�ġ��վ��롱��2��
���E������4��0�����E��8��0�����F��0��6�����F��0��10��
����E����Ϊ��4��0��ʱ��
��0����![]() ��4+b��
��4+b��
��b��3��
���F��0��3����
���߶�EF���ı���ABCD�ġ������롱��![]() ��
��
����E����Ϊ��8��0��ʱ��
��0����![]() ��8+b��
��8+b��
��b��6��
���F��0��6����
���߶�EF���ı���ABCD�ġ������롱��![]() ��
��
����F����Ϊ��0��6��ʱ��
��b��6��
��y����![]() x+6��
x+6��
���E��8��0����
���߶�EF���ı���ABCD�ġ������롱��![]() ��
��
����F����Ϊ��0��10��ʱ��
��b��10��
��y����![]() x+10��
x+10��
���E��![]() ��0��
��0��
���߶�EF���ı���ABCD�ġ������롱��![]() ��
��
��3����ͼ����ֱ��y����6��AB���ڵ�N����AC�ڵ�E��

��M��m����6�����뾶Ϊ1��
�൱��M��y�����ʱ��MN��2ʱ����M���ABC�ġ��վ��롱����1��
��m����8��4��
����M��y���Ҳ�ʱ��ME��2![]() ʱ����M���ABC�ġ��վ��롱����1��
ʱ����M���ABC�ġ��վ��롱����1��
��m��6+![]() ��6��3
��6��3![]() ��
��
�൱m����8��6+![]() ��4��m��6��3
��4��m��6��3![]() ʱ����M���ABC�ġ��վ��롱����1��
ʱ����M���ABC�ġ��վ��롱����1��