题目内容
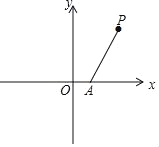
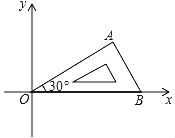
【题目】将含有 30°角的直角三角板 OAB 如图放置在平面直角坐标系中,OB 在 x轴上,若 OA=2,将三角板绕原点 O 顺时针旋转 75°,则点 A 的对应点 A′ 的坐标为___________.
【答案】(![]() ,
,![]() )
)
【解析】
过A′作A′C⊥x轴于C,根据旋转得出∠AOA′=75°,OA=OA′=2,求出∠A′OC=45°,推出OC=A′C,解直角三角形求出OC和A′C,即可得出答案.
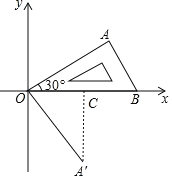
如图,过A′作A′C⊥x轴于C,
∵将三角板绕原点O顺时针旋转75°,
∴∠AOA′=75°,OA=OA′=2,
∵∠AOB=30°,
∴∠A′OC=45°,
∴OC=A′C=OA′sin45°=2×![]() =
=![]() ,
,
∴A′的坐标为(![]() ,-
,-![]() ).
).
故答案为:(![]() ,
,![]() ).
).

练习册系列答案
相关题目