题目内容
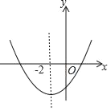
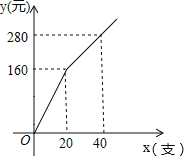
【题目】某校九年级决定购买学习用具对在本次适应性考以中成绩突出的同学进行奖励,其中计划购买,A、B两种型号的钢笔共45支,已知A种钢笔的单价为7元/支,购买B种钢笔所需费用y(元)与购买数量x(支)之间存在如图所示的函数关系式.
(1)求y与x的函数关系式;
(2)若购买计划中,B种钢笔的数最不超过35支,但不少于A种钢笔的数量,请设计购买方案,使总费用最低,并求出最低费用.
【答案】(1)y=![]() ;(2)当购买A种钢笔10支,B种钢笔35支时总费用最低,最低费用是320元.
;(2)当购买A种钢笔10支,B种钢笔35支时总费用最低,最低费用是320元.
【解析】
(1)根据函数图象中的数据可以求得y与x的函数关系式;
(2)根据(1)中的函数关系式和题意,可以求得费用的最小值和所对应的的购买方案.
解:(1)当0≤x≤20时,设y与x的函数关系式为y=k1x,
20k1=160,
解得,k1=8,
即当0≤x≤20时,y与x的函数关系式为y=8x,
当20<x≤45时,设y与x的函数关系式是y=k2x+b,
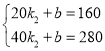 ,解得
,解得![]() ,
,
即当20<x≤45时,y与x的函数关系式是y=6x+40,
综上可知:y与x的函数关系式为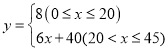 ;
;
(2)设购买B种钢笔x支,
∵B种钢笔的数最不超过35支,但不少于A种钢笔的数量,
![]() ,
,
解得22.5≤x≤35,
∵x为整数,
∴23≤x≤35,
设总费用为W元,
当23≤x≤35时,
W=8(45﹣x)+8x=360,
当20<x≤35时,
W=7(45﹣x)+(6x+40)=355﹣x,
以为k=﹣1<0,所以W随x的增大而减小,
故当x=35时,W取得最小值,此时W=320,45﹣x=10,
答:当购买A种钢笔10支,B种钢笔35支时总费用最低,最低费用是320元.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目