题目内容
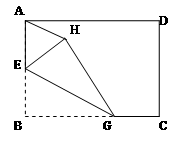
如图,正方形ABCD中,点E、F分别在边BC、CD上,且AE=EF=FA．你能得出的结论（至少写两个）是
① ② ③ （写对一个给1分，写对两个给3分）
① ② ③ （写对一个给1分，写对两个给3分）
①△ABE≌△ADF(与全等有关的结论但不是已知条件如正方形边长相等、四角为90度)；②CE=CF；③∠AEB=75°；④S△ABE＋S△ADF =S△CEF等
解：①∵AB=AD，AE=AF=EF，
∴△ABE≌△ADF（HL），∴△AEF为等边三角形，
②∴BE=DF，又BC=CD，
∴CE=CF，
③∴∠BAE=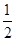
（∠BAD-∠EAF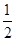）= （90°-60°）=15°，
∴∠AEB=90°-∠BAE=75°
④∵S△ABE+S△ADF=2×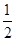 AD×DF= 
，
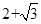S△CEF=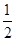 CE×CF= 
= ，
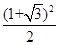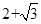∴△ABE≌△ADF（HL），∴△AEF为等边三角形，
②∴BE=DF，又BC=CD，
∴CE=CF，
③∴∠BAE=
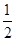（∠BAD-∠EAF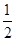）= （90°-60°）=15°，∴∠AEB=90°-∠BAE=75°
④∵S△ABE+S△ADF=2×
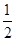AD×DF= 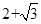，S△CEF=
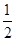CE×CF= = ，
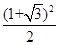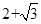练习册系列答案
相关题目
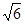
，则下底BC的长为 ．
