题目内容
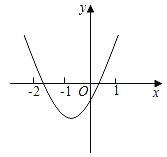
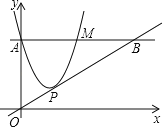
【题目】如图，在平面直角坐标系中，抛物线y＝ax2﹣2ax+
（a＞0）与y轴交于点A，过点A作x轴的平行线交抛物线于点M．P为抛物线的顶点．若直线OP交直线AM于点B，且M为线段AB的中点，则a的值为_____．
【答案】2
【解析】
先根据抛物线解析式求出点A的坐标和其对称轴，再根据对称性求出点M的坐标，利用点M为线段AB中点，得出点B的坐标；用含a的式子表示出点P的坐标，写出直线OP的解析式，再将点B的坐标代入即可求得答案.
∵抛物线y＝ax2﹣2ax+
（a＞0）与y轴交于点A，
∴A（0，），抛物线的对称轴为x＝1
∴顶点P坐标为（1，﹣a），点M坐标为（2，）
∵点M为线段AB的中点，
∴点B坐标为（4，）
设直线OP解析式为y＝kx（k为常数，且k≠0）
将点P（1，
）代入y＝kx得＝k
∴直线OP解析式为：y＝（
）x
将点B（4，）代入y＝（）x得＝（）×4
解得：a＝2
故答案为：2．
练习册系列答案
相关题目
