题目内容
【题目】已知AB是⊙O的直径,C,D是⊙O上AB同侧两点,∠BAC=26°.
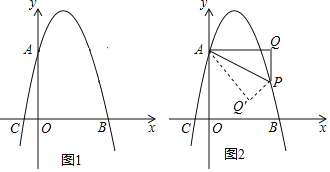
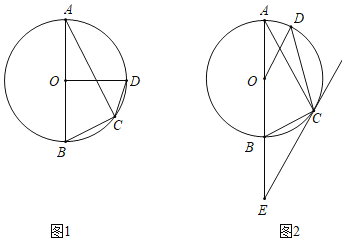
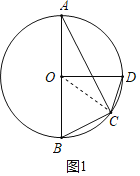
(Ⅰ)如图1,若OD⊥AB,求∠ABC和∠ODC的大小;
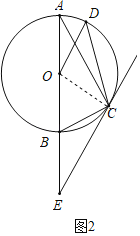
(Ⅱ)如图2,过点C作⊙O的切线,交AB的延长线于点E,若OD∥EC,求∠ACD的大小.
【答案】(Ⅰ)∠ABC=64°,∠ODC=71°;(Ⅱ)∠ACD=19°.
【解析】
(I)连接OC,根据圆周角定理得到∠ACB=90°,根据三角形的内角和得到∠ABC=65°,由等腰三角形的性质得到∠OCD=∠OCA+∠ACD=70°,于是得到结论;
(II)如图2,连接OC,根据圆周角定理和切线的性质即可得到结论.
解:(Ⅰ)连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=26°,
∴∠ABC=64°,
∵OD⊥AB,
∴∠AOD=90°,
∴∠ACD=![]() ∠AOD=
∠AOD=![]() ×90°=45°,
×90°=45°,
∵OA=OC,
∴∠OAC=∠OCA=26°,
∴∠OCD=∠OCA+∠ACD=71°,
∵OD=OC,
∴∠ODC=∠OCD=71°;
(Ⅱ)如图2,连接OC,
∵∠BAC=26°,
∴∠EOC=2∠A=52°,
∵CE是⊙O的切线,
∴∠OCE=90°,
∴∠E=38°,
∵OD∥CE,
∴∠AOD=∠E=38°,
∴∠ACD=![]() AOD=19°.
AOD=19°.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目