题目内容
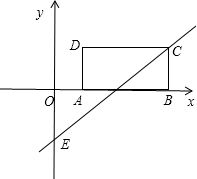
如图所示,矩形ABCD的边AB=3,AD=2,将此矩形置入直角坐标系中,使AB在x轴上,点C在直线y=x-2上.
(1)求矩形各顶点坐标;
(2)若直线y=x-2与y轴交于点E,抛物线过E、A、B三点,求抛物线的关系式;
(3)判断上述抛物线的顶点是否落在矩形ABCD内部,并说明理由.
(1)求矩形各顶点坐标;
(2)若直线y=x-2与y轴交于点E,抛物线过E、A、B三点,求抛物线的关系式;
(3)判断上述抛物线的顶点是否落在矩形ABCD内部,并说明理由.

(1)如答图所示.
∵y=x-2,AD=BC=2,设C点坐标为(m,2),
把C(m,2)代入y=x-2,
即2=m-2,
∴m=4,
∴C(4,2),
∴OB=4,AB=3,
∴OA=4-3=1,
∴A(1,0),B(4,0),C(4,2),D(1,2).
(2)∵y=x-2,
∴令x=0,得y=-2,
∴E(0,-2).
设经过E(0,-2),A(1,0),B(4,0)三点的抛物线关系式为y=ax2+bx+c,
∴
,
解得
;
∴y=-
x2+
x-2.
(3)抛物线顶点在矩形ABCD内部.
∵y=-
x2+
x-2,
∴顶点为(
,
),
∵1<
<4,
∴顶点(
,
)在矩形ABCD内部.
∵y=x-2,AD=BC=2,设C点坐标为(m,2),
把C(m,2)代入y=x-2,
即2=m-2,
∴m=4,
∴C(4,2),
∴OB=4,AB=3,
∴OA=4-3=1,
∴A(1,0),B(4,0),C(4,2),D(1,2).
(2)∵y=x-2,
∴令x=0,得y=-2,
∴E(0,-2).
设经过E(0,-2),A(1,0),B(4,0)三点的抛物线关系式为y=ax2+bx+c,
∴
|
解得
|
∴y=-
| 1 |
| 2 |
| 5 |
| 2 |
(3)抛物线顶点在矩形ABCD内部.
∵y=-
| 1 |
| 2 |
| 5 |
| 2 |
∴顶点为(
| 5 |
| 2 |
| 9 |
| 8 |
∵1<
| 5 |
| 2 |
∴顶点(
| 5 |
| 2 |
| 9 |
| 8 |

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目


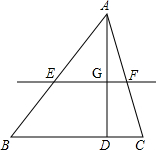 EF为斜边作等腰直角三角形PEF(点P与点A在直线EF的异侧),设EF为x,△PEF与四边形BCEF重合部分的面积为y.
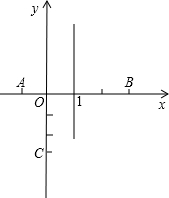
EF为斜边作等腰直角三角形PEF(点P与点A在直线EF的异侧),设EF为x,△PEF与四边形BCEF重合部分的面积为y.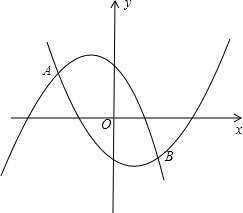 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? 们的长度(可用含m的式子表示);若不存在,请说明理由;
们的长度(可用含m的式子表示);若不存在,请说明理由;