题目内容
已知:
(1)a>0
(2)当-1≤x≤1时,满足|ax2+bx+c|≤1;
(3)当-1≤x≤1时,ax+b有最大值2.
求常数a、b、c.
(1)a>0
(2)当-1≤x≤1时,满足|ax2+bx+c|≤1;
(3)当-1≤x≤1时,ax+b有最大值2.
求常数a、b、c.
当a>0时,ax+b的值随着x取值的增大而增大,
所以x=1时,ax+b有最大值a+b,即:a+b=2
令x=0,则|c|≤1,即:-1≤c≤1
令x=1,则|a+b+c|≤1,即:|2+c|≤1,
所以-3≤c≤-1
故c=-1.
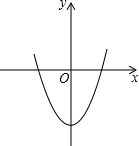
令y=ax2+bx+c,则抛物线y=ax2+bx+c必过(0,-1)
因为当-1≤x≤1时,-1≤ax2+bx+c≤1,所以该二次函数的最小值是-1,
∴
=-1
∴4ac-b2=-4a
∵c=-1
-4a-b2=-4a
∴b=0
∴a=2
所以a=2,b=0,c=-1.
所以x=1时,ax+b有最大值a+b,即:a+b=2
令x=0,则|c|≤1,即:-1≤c≤1
令x=1,则|a+b+c|≤1,即:|2+c|≤1,
所以-3≤c≤-1
故c=-1.
令y=ax2+bx+c,则抛物线y=ax2+bx+c必过(0,-1)
因为当-1≤x≤1时,-1≤ax2+bx+c≤1,所以该二次函数的最小值是-1,
∴
| 4ac-b2 |
| 4a |
∴4ac-b2=-4a
∵c=-1
-4a-b2=-4a
∴b=0
∴a=2
所以a=2,b=0,c=-1.


练习册系列答案
相关题目
 与x轴的正半轴重合,点B的对应点为点A.
与x轴的正半轴重合,点B的对应点为点A.