题目内容
如图所示的平面直角坐标系中,有一条抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为x=1,B(3,0),C(0,-3).
(1)求二次函数y=ax2+bx+c的解析式;
(2)在抛物线对称轴上是否存在一点P,使点P到A、C两点距离之和最小?若存在,求出P点坐标;若不存在,请说明理由.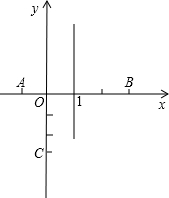
(1)求二次函数y=ax2+bx+c的解析式;
(2)在抛物线对称轴上是否存在一点P,使点P到A、C两点距离之和最小?若存在,求出P点坐标;若不存在,请说明理由.

(1)∵抛物线的对称轴为x=1,B(3,0),C(0,-3),
∴
,
解得:
,
∴二次函数y=ax2+bx+c的解析式为:y=x2-2x-3;
(2)存在.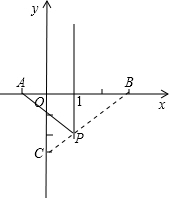
令y=0,即x2-2x-3=0,
解得:x=3或x=-1,
∴点A(-1,0),
∵点A与B关于x=1对称,
∴连接BC,则直线BC与直线x=1的交点即为P点,
设直线BC的解析式为y=kx+b,
∴
,
解得:
,
∴直线BC的解析式为y=x-3,
当x=1时,y=1-3=-2,
∴点P的坐标为(1,-2).
∴
|
解得:
|
∴二次函数y=ax2+bx+c的解析式为:y=x2-2x-3;
(2)存在.

令y=0,即x2-2x-3=0,
解得:x=3或x=-1,
∴点A(-1,0),
∵点A与B关于x=1对称,
∴连接BC,则直线BC与直线x=1的交点即为P点,
设直线BC的解析式为y=kx+b,
∴
|
解得:
|
∴直线BC的解析式为y=x-3,
当x=1时,y=1-3=-2,
∴点P的坐标为(1,-2).

练习册系列答案
相关题目