题目内容
如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),B(4,0),与y轴交于点C(0,-2).
(1)求此抛物线的解析式;
(2)若D点在此抛物线上,且AD∥CB,在x轴上是否存在点E,使得以A,D,E为顶点的三角形与△ABC相似?若存在,求出点E的坐标;若不存在,请说明理由;
(3)在(2)的条件下,问在x轴下方的抛物线上,是否存在点P使得△APD的面积与四边形ACBD的面积相等?若存在,求出P点坐标;若不存在,请说明理由.

(1)求此抛物线的解析式;
(2)若D点在此抛物线上,且AD∥CB,在x轴上是否存在点E,使得以A,D,E为顶点的三角形与△ABC相似?若存在,求出点E的坐标;若不存在,请说明理由;
(3)在(2)的条件下,问在x轴下方的抛物线上,是否存在点P使得△APD的面积与四边形ACBD的面积相等?若存在,求出P点坐标;若不存在,请说明理由.

(1)∵抛物线y=ax2+bx+c与x轴交于点A(-1,0),B(4,0),与y轴交于点C(0,-2),
∴
,
解得:
,
∴抛物线的解析式为y=
x2-
x-2;
(2)设D点坐标为(x,y),E点坐标为(a,0)
∵AD∥CB,
∴两直线的斜率相等,
∴kAD=kBC,
∴
=
=
,
∴y+1=
x,
又∵点D在抛物线上,
∴y=
x2-
x-2,
联立两式解得D点的坐标为(5,3),
连接AC,AC=
,BC=2
,AB=5,
∵AC2+BC2=AB2,
∴△ACB是直角三角形,
①若Rt△ACB∽RtEDA,如图1所示,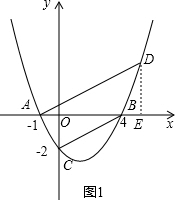
∵AD∥AC,
∴∠DAB=∠ABC,
∵Rt△ACB∽RtEDA,
∴
=
=
,
∴
=
=
,
当a=5时,等式成立,
∴当E点坐标为(5,0)时,Rt△ACB∽RtAED;
②若Rt△ACB∽RtADE,如图2所示,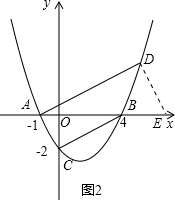
同理可知
=
,即
=
,
解得a=
,
∴AE=
,根据勾股定理求出DE=
,
检验:
=
=
,
∴存在E点坐标(
,0)使以A,D,E为顶点的三角形与△ABC相似,
综上这样的点有两个,分别是(5,0),(
,0);
(3)由(1)(2)可知:AB=5,D点坐标为(5,3),C点坐标为(0,-2),
假设存在P点(x,y)使得△APD的面积与四边形ACBD的面积相等,
S四边形ACBD=S△ABD+S△ACB=
×5×3+
×5×2=
,
S△APD=
×AD×h=
,解得h=
,
∴P到直线AD的距离为
,
直线AD的解析式为y=
x+
,
P点到直线AD的距离d=
=
,
又知y=
x2-
x-2,
解得x=
∴这样的P点存在,坐标为(
,
)、(
,
).
∴
|
解得:
|
∴抛物线的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)设D点坐标为(x,y),E点坐标为(a,0)
∵AD∥CB,
∴两直线的斜率相等,
∴kAD=kBC,
∴
| y+1 |
| x |
| 0-(-2) |
| 4-0 |
| 1 |
| 2 |
∴y+1=
| 1 |
| 2 |
又∵点D在抛物线上,
∴y=
| 1 |
| 2 |
| 3 |
| 2 |
联立两式解得D点的坐标为(5,3),
连接AC,AC=
| 5 |
| 5 |
∵AC2+BC2=AB2,
∴△ACB是直角三角形,
①若Rt△ACB∽RtEDA,如图1所示,

∵AD∥AC,
∴∠DAB=∠ABC,
∵Rt△ACB∽RtEDA,
∴
| AC |
| DE |
| AB |
| AD |
| BC |
| AE |
∴
| ||
| 3 |
| 5 | ||
3
|
2
| ||
| a+1 |
当a=5时,等式成立,
∴当E点坐标为(5,0)时,Rt△ACB∽RtAED;
②若Rt△ACB∽RtADE,如图2所示,

同理可知
| AB |
| AE |
| AC |
| AD |
2
| ||
3
|
| 5 |
| a+1 |
解得a=
| 13 |
| 2 |
∴AE=
| 15 |
| 2 |
3
| ||
| 2 |
检验:
| AC |
| DE |
| AB |
| AE |
| 2 |
| 3 |
∴存在E点坐标(
| 13 |
| 2 |
综上这样的点有两个,分别是(5,0),(
| 13 |
| 2 |
(3)由(1)(2)可知:AB=5,D点坐标为(5,3),C点坐标为(0,-2),
假设存在P点(x,y)使得△APD的面积与四边形ACBD的面积相等,
S四边形ACBD=S△ABD+S△ACB=
| 1 |
| 2 |
| 1 |
| 2 |
| 25 |
| 2 |
S△APD=
| 1 |
| 2 |
| 25 |
| 2 |
5
| ||
| 3 |
∴P到直线AD的距离为
5
| ||
| 3 |
直线AD的解析式为y=
| 1 |
| 2 |
| 1 |
| 2 |
P点到直线AD的距离d=
| |x-2y+1| | ||
|
5
| ||
| 3 |
又知y=
| 1 |
| 2 |
| 3 |
| 2 |
解得x=
6±2
| ||
| 3 |
∴这样的P点存在,坐标为(
6+2
| ||
| 3 |
51-3
| ||
| 9 |
6-2
| ||
| 3 |
51-21
| ||
| 9 |

练习册系列答案
相关题目
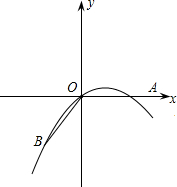 与x轴的正半轴重合,点B的对应点为点A.
与x轴的正半轴重合,点B的对应点为点A.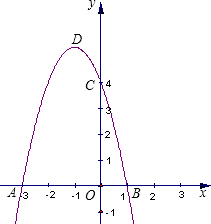 点C,其中点A的坐标为(-3,0),
点C,其中点A的坐标为(-3,0),