题目内容
如图,△ABC的高AD为3,BC为4,直线EF∥BC,交线段AB于E,交线段AC于F,交AD于G,以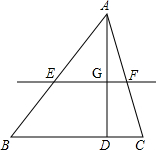 EF为斜边作等腰直角三角形PEF(点P与点A在直线EF的异侧),设EF为x,△PEF与四边形BCEF重合部分的面积为y.
EF为斜边作等腰直角三角形PEF(点P与点A在直线EF的异侧),设EF为x,△PEF与四边形BCEF重合部分的面积为y.
(1)求线段AG(用x表示);
(2)求y与x的函数关系式,并求x的取值范围.
 EF为斜边作等腰直角三角形PEF(点P与点A在直线EF的异侧),设EF为x,△PEF与四边形BCEF重合部分的面积为y.
EF为斜边作等腰直角三角形PEF(点P与点A在直线EF的异侧),设EF为x,△PEF与四边形BCEF重合部分的面积为y.(1)求线段AG(用x表示);
(2)求y与x的函数关系式,并求x的取值范围.
(1)∵EF∥BC,
∴△AEF∽△ABC,
∴
=
,
∴
=
,AG=
x.
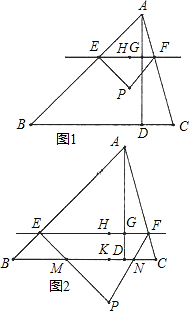
(2)当点P在四边形BCFE的内部或BC边上时,如图1过点P作PH⊥EF于H,
∵等腰直角三角形PEF,
∴PH=
x,
∴y=
EF×PH=
x2.
∵PH≤DG,
x≤3-
x,0<x≤
.
当点P在四边形BCFE的外部时,如图2,
过点P作PH⊥EF于H,交MN于K,同理得PH=
x,
∵EF∥BC,
∴∠KHG=∠HKD=90°,
∴四边形HGDK为矩形,
∴HK=DG=3-
x,
∴PK=
x-(3-
x)=
x-3,
∵EF∥BC,
∴△PMN∽△PEF,
∴
=
,
∴△PMN为等腰直角三角形.
∴S△PMN=
MN×PK=PK2=(
x-3)2=
x2-
x+9,
∴y=
x2-(
x2-
x+9)=-
x2+
x-9,
∵PH>DG,
x>3-
x,x>
∴
<x<4.
∴△AEF∽△ABC,
∴
| EF |
| BC |
| AG |
| AD |
∴
| x |
| 4 |
| AG |
| 3 |
| 3 |
| 4 |
(2)当点P在四边形BCFE的内部或BC边上时,如图1过点P作PH⊥EF于H,
∵等腰直角三角形PEF,
∴PH=
| 1 |
| 2 |
∴y=
| 1 |
| 2 |
| 1 |
| 4 |
∵PH≤DG,
| 1 |
| 2 |
| 3 |
| 4 |
| 12 |
| 5 |
当点P在四边形BCFE的外部时,如图2,
过点P作PH⊥EF于H,交MN于K,同理得PH=
| 1 |
| 2 |
∵EF∥BC,
∴∠KHG=∠HKD=90°,
∴四边形HGDK为矩形,
∴HK=DG=3-
| 3 |
| 4 |
∴PK=
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 4 |
∵EF∥BC,
∴△PMN∽△PEF,
∴
| PM |
| PE |
| PN |
| PF |
∴△PMN为等腰直角三角形.
∴S△PMN=
| 1 |
| 2 |
| 5 |
| 4 |
| 25 |
| 16 |
| 15 |
| 2 |
∴y=
| 1 |
| 4 |
| 25 |
| 16 |
| 15 |
| 2 |
| 21 |
| 16 |
| 15 |
| 2 |
∵PH>DG,
| 1 |
| 2 |
| 3 |
| 4 |
| 12 |
| 5 |
∴
| 12 |
| 5 |


练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目

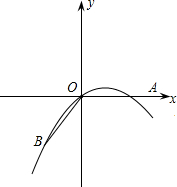 与x轴的正半轴重合,点B的对应点为点A.
与x轴的正半轴重合,点B的对应点为点A.
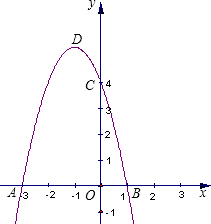 点C,其中点A的坐标为(-3,0),
点C,其中点A的坐标为(-3,0),