题目内容
【题目】如图,在
中,
垂足分别为Q、S．
（1）试说明：
≌
；
（2）若QS=3.5cm，NQ=2.1cm ,求MS的长．
【答案】（1）见解析；（2）5.6cm．
【解析】
（1）求出∠PSM=∠Q=∠MPN=90°，∠PMS=∠NPQ，根据AAS证出全等即可；
（2）根据全等得出MS=PQ，PS=NQ=2.1cm，代入MS=PQ=QS+PS求出即可．
（1）解：∵∠MPN=90°，NQ⊥PQ，MS⊥PQ，
∴∠PSM=∠Q=∠MPN=90°，
∴∠SPM+∠PMS=90°，∠SPM+∠NPQ=90°，
∴∠PMS=∠NPQ，
在△PMS和△NPQ中
，
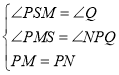∴△PMS≌△NPQ（AAS）；
（2）解：∵△PMS≌△NPQ，
∴MS=PQ，PS=NQ，
∵NQ=2.1cm，
∴PS=2.1cm，
∴MS=PQ=QS+PS=2.1cm+3.5cm=5.6cm．
练习册系列答案
相关题目
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共
个，小李做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，如表是实验中的一组统计数据：
摸球的次数 |
|
|
|
|
|
|
|
摸到白球的次数 |
|
|
|
|
|
|
|
摸到白球的频率 |
|
|
|
|
|
|
|
请估计：当实验次数为
次时，摸到白球的频率将会接近________；（精确到
）
假如你摸一次，你摸到白球的概率
（摸到白球）
________；
如何通过增加或减少这个不透明盒子内球的具体数量，使得在这个盒子里每次摸到白球的概率为
？
