题目内容
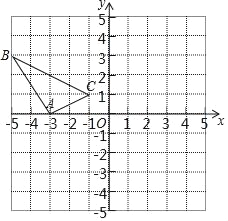
【题目】如图1,在Rt△ABC中,∠ACB=90°,动点M从点A出发沿A-C-B向点B匀速运动,动点N从点B出发沿B-C-A向点A运动.设MC的长为y1(cm),NC的长为y2(cm),点M的运动时间为x(s);y1、y2与x的函数图像如图2所示.

(1)线段AC= cm,点M运动 s后点N开始运动;
(2)求点P的坐标,并写出它的实际意义;
(3)当∠CMN=45°时,求x的值.
【答案】(1)10,1;(2)P为(![]() ,0);点P的实际意义为:点M运动到点C,MC=0;(3)当∠CMN=45°时,x的值为2或4.
,0);点P的实际意义为:点M运动到点C,MC=0;(3)当∠CMN=45°时,x的值为2或4.
【解析】
(1)由函数图像可知,AC=10,点M运动1秒后,点N开始运动;
(2)由点M为匀速运动,则先计算点M的速度,然后求出点M运动到点C时的时间,即求出点P的坐标;
(3)先求出点N在BC上的运动速度和在AC上的运动速度,结合∠CMN=45°,则CM=CN,可分为两种情况进行①点M在AC上,点N在BC上;②点M在BC上,点N在AC上;分别列式求解即可.
解:(1)根据函数的图像可知,
当点M与点A重合时,AC=MC=10cm,
当点N与点B重合时,BC=NC=8cm,
由图可知,点M运动1秒后,点N开始运动,
故答案为:10,1;
(2)由题意,点M为匀速运动,则
点M的速度为:![]() ,
,
∴当点M运动到点C时,MC=0,则
点P的横坐标为:![]() ,
,
∴点P的坐标为:(![]() ,0);
,0);
点P的实际意义为:点M运动到点C,MC=0;
(3)由图可知,点N在BC上运动的速度为:![]() ,
,
点N在AC上运动的速度为:![]() ;
;
∵∠CMN=45°,
∴△CMN是等腰直角三角形,即MC=NC,
①如图,当点M在AC上,点N在BC上时,有
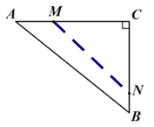
设x秒后,∠CMN=45°,
∴![]() ,
,![]() ,
,
∴![]() ,
,
解得:![]() ;
;
②如图,当点M在BC上,点N在AC上时,有
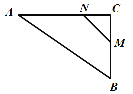
点N到达点C所用的时间为![]() ,
,
设x秒后,∠CMN=45°,
∴![]() ,
,![]() ,
,
∴![]() ,
,
解得:![]() ;
;
综合上述,当∠CMN=45°时,x的值为2或4.

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案