题目内容
如图,在平面直角坐标系中有两点 、
、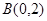 ,如果点
,如果点 在
在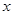 轴上(
轴上( 与
与 不重合),当点
不重合),当点 的坐标为
的坐标为
或 时,使得由点 组成的三角形与
组成的三角形与 相似(至少找出两个满足条件的点的坐标).
相似(至少找出两个满足条件的点的坐标).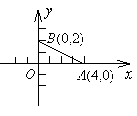
 、
、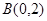 ,如果点
,如果点 在
在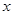 轴上(
轴上( 与
与 不重合),当点
不重合),当点 的坐标为
的坐标为 或 时,使得由点
 组成的三角形与
组成的三角形与 相似(至少找出两个满足条件的点的坐标).
相似(至少找出两个满足条件的点的坐标).
(-1,0)或(1,0)
分析:分类讨论:①当△AOB∽△COB时,求点C的坐标;②当△AOB∽△BOC时,求点C的坐标.
解:∵点C在x轴上,∴点C的纵坐标是0,且当∠BOC=90°时,由点B、O、C组成的三角形与△AOB相似,即∠BOC应该与∠BOA=90°对应,
①当△AOB∽△COB,即OC与OA相对应时,则OC=OA=4,C(-4,0);
②当△AOB∽△BOC,即OC与OB对应,则OC=1,C(-1,0)或者(1,0).
故答案可以是:(-1,0);(1,0).

练习册系列答案
相关题目
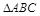 ∽
∽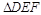 ,若AB:DE=2:1,且
,若AB:DE=2:1,且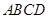 中,
中,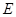 是边
是边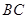 上的点,
上的点,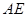 交
交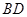 于点
于点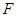 ,如果
,如果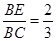 ,那么
,那么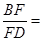 .
.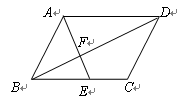
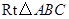 中,
中,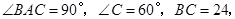 点
点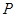 是
是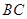 边上的动点(点
边上的动点(点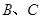 不重合),过动点
不重合),过动点 交
交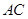 于点
于点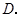
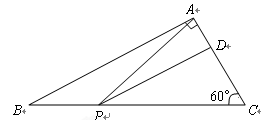
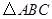 与
与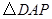 相似,则
相似,则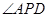 是多少度?
是多少度?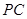 等于多少时,
等于多少时,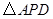 的面积最大?最大面积是多少?
的面积最大?最大面积是多少? 为直径的圆相外切,
为直径的圆相外切,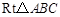 中,
中,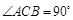 ,
,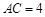 ,
,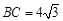 ,以
,以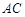 为直径的⊙O交
为直径的⊙O交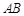 于点
于点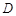 ,点
,点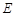 是
是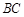 的中点,OB,DE相交于点F。
的中点,OB,DE相交于点F。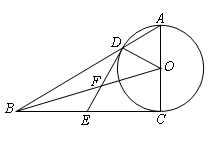
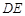 是⊙O的切线;
是⊙O的切线;