题目内容
【题目】如图,在![]() 中,
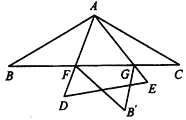
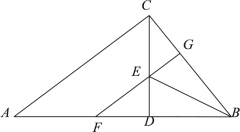
中,![]() ,CD是高,BE平分∠ABC交CD于点E,EF∥AC交AB于点F,交BC于点G.在结论:(1)
,CD是高,BE平分∠ABC交CD于点E,EF∥AC交AB于点F,交BC于点G.在结论:(1) ![]()
![]() ;(2)
;(2) ![]() ;(3)
;(3)![]() ;(4)
;(4) ![]() 中,一定成立的有( )
中,一定成立的有( )
A.1个B.2个C.3个D.4个
【答案】B
【解析】
根据两直线平行,同旁内角互补求出∠CGE=∠BCA=90°,然后根据等角的余角相等即可求出∠EFD=∠BCD;只有△ABC是等腰直角三角形时AD=CD,CG=EG;利用“角角边”证明△BCE和△BFE全等,然后根据全等三角形对应边相等可得BF=BC.
∵EF∥AC,∠BCA=90°,
∴∠CGE=∠BCA=90°,
∴∠BCD+∠CEG=90°,
又∵CD是高,
∴∠EFD+∠FED=90°,
∵∠CEG=∠FED(对顶角相等),
∴∠EFD=∠BCD,故(1)正确;
只有∠A=45°,即△ABC是等腰直角三角形时,AD=CD,CG=EG而立,故(2)(3)不一定成立,错误;
∵BE平分∠ABC,
∴∠EBC=∠EBF,
在△BCE和△BFE中,
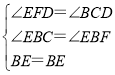 ,
,
∴△BCE≌△BFE(AAS),
∴BF=BC,故(4)正确,
综上所述,正确的有(1)(4)共2个.
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目