题目内容
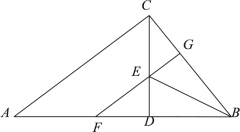
【题目】如图，△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB，DE与AC、AE分别交于点O、点E，连接EC．
（1）求证：AD=EC；
（2）当∠BAC=Rt∠时，求证：四边形ADCE是菱形．
【答案】（1）见解析；
（2）见解析.
【解析】
（1）先证四边形ABDE是平行四边形，再证四边形ADCE是平行四边形即可；
（2）由∠BAC=90°，AD是边BC上的中线，得AD=BD=CD，即可证明.
(1)证明：∵AE∥BC，DE∥AB ，
∴四边形ABDE是平行四边形，
∴AE=BD，
∵AD是边BC上的中线，
∴BD=DC，
∴AE=DC，
又∵AE∥BC，
∴四边形ADCE是平行四边形.
(2) 证明：∵∠BAC=90°，AD是边BC上的中线.
∴AD=CD
∵四边形ADCE是平行四边形，
∴四边形ADCE是菱形.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某中学开展“英语演讲”比赛活动，八年级（1），（2）班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩（满分为100分）如图所示，
（1）根据图示填写下表：
班级 | 平均数（分） | 中位数（分） | 众数（分） |
八（1） | ______ | 85 | ______ |
八（2） | 85 | ______ | 100 |
（2）计算两班复赛成绩的方差并说明哪版的成绩比较稳定．（方差公式：S2=
]）
