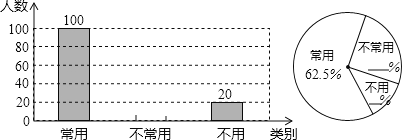
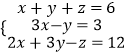��Ŀ����
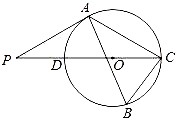
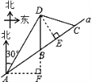
����Ŀ����ͼ��ij�н��⾰����һ����ֱ�Ĺ�·a������������A��B��C��������ί���ֿ����˷羰�����ľ���D������������Dλ�ھ���A�ı�ƫ��30������8km����λ�ھ���B����������λ�ھ���C�ı�ƫ��75�������ϣ���֪AB=5km��

��1��������ί�����ɾ���D��·a��һ��������̵Ĺ�·���������������أ����������·�ij����������ȷ��0.1km��
��2����C�뾰��D֮��ľ��룮�������ȷ��1km��
���ο����ݣ�![]() =1.73��
=1.73��![]() =2.24��sin53��=cos37��=0.80��sin37��=cos53��=0.60��tan53��=1.33��tan37��=0.75��sin38��=cos52��=0.62��sin52��=cos38��=0.79��tan38��=0.78��tan52��=1.28��sin75��=0.97��cos75��=0.26��tan75��=3.73����
=2.24��sin53��=cos37��=0.80��sin37��=cos53��=0.60��tan53��=1.33��tan37��=0.75��sin38��=cos52��=0.62��sin52��=cos38��=0.79��tan38��=0.78��tan52��=1.28��sin75��=0.97��cos75��=0.26��tan75��=3.73����
���𰸡���1��3.1km����2��4km��
���������⣺��1����ͼ������D��DE��AC�ڵ�E��
����A��AF��DB����DB���ӳ����ڵ�F����Rt��DAF�У���ADF=30����
��AF=![]() AD=
AD=![]() ��8=4����DF=
��8=4����DF=![]() ��
��
��Rt��ABF��BF=![]() =3��
=3��
��BD=DF��BF=4![]() ��3��sin��ABF=
��3��sin��ABF=![]() ��
��
��Rt��DBE�У�sin��DBE=![]() ���ߡ�ABF=��DBE����sin��DBE=
���ߡ�ABF=��DBE����sin��DBE=![]() ��
��
��DE=BDsin��DBE=![]() ����4
����4![]() ��3��=
��3��=![]() ��3.1��km����
��3.1��km����
�ྰ��D��·a����������·�ij�Լ��3.1km��
��2���������֪��CDB=75����
�ɣ�1����֪sin��DBE=![]() =0.8�����ԡ�DBE=53����
=0.8�����ԡ�DBE=53����
���DCB=180�㩁75�㩁53��=52����
��Rt��DCE��sin��DCE=![]() ����DC=
����DC=![]() ��4��km����
��4��km����
�ྰ��C�뾰��D֮��ľ���ԼΪ4km��

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ����֪���κ���y��ax2+bx+c�У�����y���Ա���x�IJ��ֶ�Ӧֵ�������y��5ʱ��x��ȡֵ��Χ��_____��
x | �� | ��1 | 0 | 1 | 2 | 3 | �� |
y | �� | 10 | 5 | 2 | 1 | 2 | �� |