题目内容
【题目】如图, ![]() 中,
中, ![]() ,
, ![]() =120°,以
=120°,以![]() 为一个顶点的等边三角形
为一个顶点的等边三角形![]() 绕点A在
绕点A在![]() 内旋转,
内旋转, ![]() 、
、![]() 所在的直线与
所在的直线与![]() 边分别交于点
边分别交于点![]() 、
、![]() ,若点
,若点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,当
,当![]() 是以点
是以点![]() 为直角顶点的直角三角形时,
为直角顶点的直角三角形时, ![]() 的长为__
的长为__
【答案】![]()
【解析】试题解析:作AH⊥BC于H,如图1,
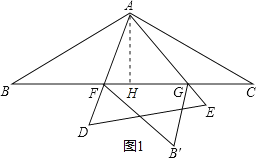
∵AB=AC=4,∠BAC=120°,
∴∠B=30°,BH=CH,
在Rt△ABH中,AH=![]() AB=2,BH=
AB=2,BH=![]() AH=2
AH=2![]() ,
,
∴BC=2BH=4![]() ,
,
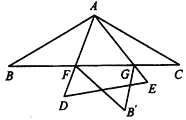
把△ACG绕点A顺时针旋转120°得到△ABG′,连结FG′、AB′,如图2,则BG′=CG,AG=AG,∠ABG′=∠C=30°,∠1=∠BAG′,

∴∠FBG′=60°,
∵∠FAG=60°,
∴∠1+∠2=60°,
∴∠FAG′=60°,
在△AFG和△AFG′中,
 ,
,
∴△AFG≌△AFG′,
∴FG=FG′,
∵点B关于直线AD的对称点为B′,
∴FB=FB′,AB=AB′,∠2=∠3,
而∠3+∠4=60°,∠1+∠2=60°,
∴∠1=∠4,
而AC=AB=AB′,
∴△AB′G与△ACG关于AG对称,
∴GB′=GC,
∴GB′=BG′,
在△FB′G和△FBG′中,
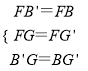 ,
,
∴△FB′G≌△FBG′,
∴∠FGB′=∠BG′F=90°,
在Rt△BFG′中,∵∠FBG′=60°,
∴BG′=![]() BF,FG′=
BF,FG′=![]() BF,
BF,
∴CG=![]() BF,FG=
BF,FG=![]() BF,
BF,
∴BF+![]() BF+
BF+![]() BF=BC=4
BF=BC=4![]() ,
,
∴BF=4![]() -4.
-4.
故答案为4![]() -4.
-4.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目