Question

【题目】设a1 ， a2 ， …，a2014是从1，0，﹣1这三个数中取值的一列数，若a1+a2+…+a2014=69，（a1+1）2+（a2+1）2+…+（a2014+1）2=4001，则a1 ， a2 ， …，a2014中为0的个数是 ．

Answer 1

【答案】165
【解析】解：（a1+1）2+（a2+1）2+…+（a2014+1）2=a12+a22+…+a20142+2（a1+a2+…+a2014）+2014
=a12+a22+…+a20142+2×69+2014
=a12+a22+…+a20142+2152，
设有x个1，y个﹣1，z个0
∴ ，
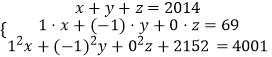化简得x﹣y=69，x+y=1849，
解得x=959，y=890，z=165
∴有959个1，890个﹣1，165个0，
所以答案是：165．
【考点精析】认真审题，首先需要了解数与式的规律(先从图形上寻找规律，然后验证规律，应用规律，即数形结合寻找规律)．