Question

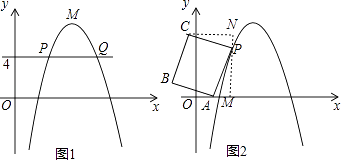
【题目】如图1，在平面直角坐标系xOy中，点M为抛物线y=﹣x2+2nx﹣n2+2n的顶点，过点（0，4）作x轴的平行线，交抛物线于点P、Q（点P在Q的左侧），PQ=4．

（1）求抛物线的函数关系式，并写出点P的坐标；
（2）小丽发现：将抛物线y=﹣x2+2nx﹣n2+2n绕着点P旋转180°，所得新抛物线的顶点恰为坐标原点O，你认为正确吗？请说明理由；
（3）如图2，已知点A（1，0），以PA为边作矩形PABC（点P、A、B、C按顺时针的方向排列）， ．
写出C点的坐标：C（ ， ）（坐标用含有t的代数式表示）；
（4）若点C在题（2）中旋转后的新抛物线上，求t的值．

Answer 1

【答案】
（1）

解：∵抛物线y=﹣x2+2nx﹣n2+2n过点P，P点的纵坐标为4，

∴4=﹣x2+2nx﹣n2+2n

解得：x1=n+ ，x2=n﹣ ，

∵PQ=x1﹣x2=4，

∴2 =4，

解得：n=4，

∴抛物线的函数关系式为：y=﹣x2+8x﹣8，

∴4=﹣x2+8x﹣8，

解得：x=2或x=6，

∴P（2，4）．

（2）

解：正确；

∵P（2，4），PQ=4，

∴Q绕着点P旋转180°后的对称点为Q′（﹣2，4），

∴P与Q′正好关于y轴对称，

∴所得新抛物线的对称轴是y轴，

∵抛物线y=﹣x2+8x﹣8=﹣（x﹣4）2+8，

∴抛物线的顶点M（4，8），

∴顶点M到直线PQ的距离为4，

∴所得新抛物线顶点到直线PQ的距离为4，

∴所得新抛物线顶点应为坐标原点．

（3）﹣4t+2；4+t
（4）

解：由（1）可知，旋转后的新抛物线是y=ax2，

∵新抛物线是y=ax2过P（2，4），

∴4=4a，

∴a=1，

∴旋转后的新抛物线是y=x2，

∵C（﹣4t+2，4+t）在抛物线y=x2上，

∴4+t=（﹣4t+2）2，

解得：t=0（舍去）或t= ，

∴t= ．

【解析】解：（3）如图2，过P作x轴的垂线，交x轴于M，过C作CN⊥MN于N，
∵ ，
∴ = ，
∵△APM∽△PCN，
∴ = = = ，
∵AM=2﹣1=1，PM=4，
∴PN=t，CN=4t，
∴MN=4+t，
∴C（﹣4t+2，4+t），
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案，需要熟知二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．