Question

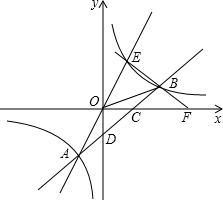
如图，直线与y=2x双曲线y=

8

x

相交于点A、E，直线AB与双曲线交于点B，与x轴、y轴分别交于点C、D，且B点横坐标等于纵坐标的两倍，直线EB交x轴于点F，
（1）求直线AB的解析式；
（2）求证：△COD∽△CBF．

Answer 1

（1）∵直线与y=2x双曲线y=

8

x

相交于点A、E，
∴

y=2x y= 8 x

，
解得：

x1=2 y1=4

，

x2=-2 y2=-4

，
∴A点坐标为：（-2，-4），E点坐标为：（2，4），
∵B点横坐标等于纵坐标的两倍，
∴设B点坐标为：（2x，x），
∴2x•x=8，
即x ²=4，
解得：x₁=2，x₂=-2（不合题意舍去），
∴B点坐标为：（4，2），
设直线AB的解析式为：y=ax+b，
故将A，B点坐标代入解析式得：

-2a+b=-4 4a+b=2

，
解得：

a=1 b=-2

，
故直线AB的解析式为：y=x-2；

（2）过点B作BM⊥OF于点M，
∵直线AB的解析式为：y=x-2，
∴y=0时，x=2，则图象与x轴交于点C（2，0），进而得出图象与y轴交于点（0，2），
∴DO=CO=2，
∴CD=2

2

，
设直线EB的解析式为：y=cx+d，
将E，B点代入得：

2c+d=4 4c+d=2

，
解得：

c=-1 d=6

，
故直线EB的解析式为：y=-x+6，
当y=0，则x=6，
故F点坐标为：（6，0），
则FC=4，
又∵B点坐标为：（4，2），CO=2，
∴MO=4，BM=2，
∴CM=2，MF=2，
∴BC=CF=2

2

，
∵

CO

BC

=

DO

BF

=

CD

FC

=

2

2 2

=

2

2

，
∴△COD∽△CBF．