Question

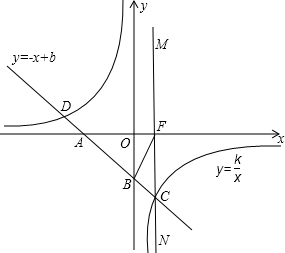
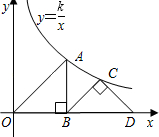
如图在等腰Rt△OBA和Rt△BCD中，∠OBA=∠BCD=90°，点A和点C都在双曲线y=

k

x

（k＞0）上，则点D的坐标为______．

Answer 1

过C点作CE⊥BD于E，如图，

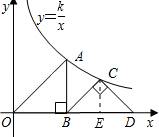
∵△OBA为等腰直角三角形，∠OBA=90°，
∴OB=AB，
设A（a，a），
∵A在反比例y=

k

x

图象上，
∴a•a=k，
∴a=

k

，或a=-

k

（舍去），即OB=

k

，
又∵△CBD为等腰直角三角形，∠BCD=90°，
∴CE=BE=DE，
设CE=b，则OE=b+

k

，OD=

k

+2b，
∴C点坐标为（b+

k

，b），
∴（b+

k

）•b=k，
解得：b=

- k + 5k

2

，或b=

- k - 5k

2

（舍去），
∴OD=

k

+2×

- k + 5k

2

=

5k

，
∴点D的坐标为（

5k

，0）．
故答案为：（

5k

，0）